Tìm STN n sao cho M =[n-2].[n2+n-1]là số nguyên tố
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PL
0
19 tháng 7 2021
1,
Đặt A = n3 - n2 + n - 1
Ta có A = n2(n - 1) + (n - 1) = (n - 1)(n2 + 1)
Vì A nguyên tố nên A chỉ có 2 Ư. Ư thứ 1 là 1 còn Ư thứ 2 nguyên tố nên ta suy ra 2 trường hợp :
TH1 : n - 1 = 1 và n2 + 1 nguyên tố
⇒
n = 2 và n2 + 1 = 5 nguyên tố (thỏa)
TH2 : n2 + 1 = 1 và n - 1 nguyên tố
⇒
n = 0 và n - 1 = - 1( ko thỏa)
Vậy n = 2
19 tháng 7 2021
2 ,
Xột số A = (2n – 1)2n(2n + 1)
A là tích của 3 số tự nhiên liờn tiệp nên A ⋮ 3
Mặt khỏc 2n – 1 là số nguyên tố ( theo giả thiết )
2n không chia hết cho 3
Vậy 2n + 1 phải chia hết cho 3 ⇒ 2n + 1 là hợp số.
SO
0
26 tháng 12 2022
\(n^2+4n=n\left(n+4\right)\)
Để n(n+4) là số nguyên tố thì (n+4;n): (4;1);(1;4);(-1;-4);(-4;-1)
Nếu n+4 = 4; n=1 => n =0 hoặc n=1
Nếu n+4=1; n=4 => n=-3 hoặc n=4
Nếu n+4 = -1;n=-4 => n = 3 hoặc n=-4
Nếu n+4= -4; n= -1 => n=-8; n=-1
DD
Đoàn Đức Hà
Giáo viên
26 tháng 12 2022
\(n^2+4n=n\left(n+4\right)\)
Để \(n^2+4n\) là số nguyên tố thì \(\left[{}\begin{matrix}n=1\\n+4=1\end{matrix}\right.\).
Với \(n=1\): \(n^2+4n=5\) (thỏa mãn).
Với \(n+4=1\Leftrightarrow n=-3\) (không thỏa mãn).
LC
0
PT
1
CM
23 tháng 6 2018
Ta có :
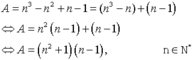
Nếu n = 1 suy ra A = 0
Nếu n = 2 suy ra A = 5 là số nguyên tố
Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số
Vậy để A = n3 – n2 + n – 1 là số nguyên tố thì n = 2.
TK
2
MN
1
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
Lời giải:
Để $p=(n-2)(n^2+n-5)$ là số nguyên tố thì bản thân 1 trong 2 thừa số $n-2, n^2+n-5$ là số nguyên tố và số còn lại bằng 1.
TH1: $n-2=1\Rightarrow n=3$. Khi đó: $p=7$ là số nguyên tố (thỏa mãn)
TH2: $n^2+n-5=1\Rightarrow n^2+n-6=0\Rightarrow (n-2)(n+3)=0$
$\Rightarrow n=2$
$\Rightarrow p=0$ không là snt (loại)
Vậy $n=3$