Biến đổi tích thành tổng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 11 2015
Theo tính chất của phép nhân đối với phép cộng ta có:
ab - ac + ad = a.(b - c + d)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
\(\begin{array}{l}1.\,\,\,\,\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right] \Leftrightarrow 2\cos a.\cos b = \cos \left( {a + b} \right) + \cos \left( {a - b} \right)\\ \Leftrightarrow 2\cos \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \cos u + \cos v\\2.\,\,\,\,\sin a.\sin b = - \frac{1}{2}.\left[ {\cos \left( {a + b} \right) - \cos \left( {a - b} \right)} \right] \Leftrightarrow - 2.\sin a.\sin b = \cos \left( {a + b} \right) - \cos \left( {a - b} \right)\\ \Leftrightarrow - 2.\sin \frac{{u + v}}{2}.\sin \frac{{u - v}}{2} = \cos u - \cos v\\3.\,\,\,\,\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right] \Leftrightarrow 2\sin a.\cos b = \sin \left( {a + b} \right) + \sin \left( {a - b} \right)\\ \Leftrightarrow 2\sin \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \sin u + \sin v\\4.\,\,\,\,\sin \left( {a + b} \right) - \sin \left( {a - b} \right) = \sin a.\cos b + \cos a.\sin b - \sin a.\cos b + \cos a.\sin b = 2\cos a.\sin b\\ \Leftrightarrow \sin u - \sin v = 2.\cos \frac{{u + v}}{2}.\sin \frac{{u - v}}{2}\end{array}\)
HP
20 tháng 9 2021
(3x - 1)2 - (2x - 5)2
= (3x - 1 - 2x + 5)(3x - 1 + 2x - 5)
= (x + 4)(5x - 6)
20 tháng 9 2021
\(\left(3x-1\right)^2-\left(2x-5\right)^2\)
\(=\left(3x-1-2x+5\right)\left(3x-1+2x-5\right)\)
\(=\left(x+4\right)\left(5x-6\right)\)
TT
3
CM
12 tháng 1 2017
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
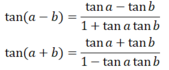
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
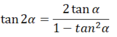
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
HP
1
6 tháng 9 2015
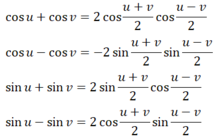
= 11 x 11 + 11 x 12 + 11 x 13 + 25 x 11 = 11 x (11 + 12 + 13 + 25) = 11 x 61
VT
3
IW
16 tháng 5 2016
Ta có: 24.24+28.28+48.48
= 24.24+(24+4).(24+4)+(24+24).(24+24)
=24.24+24.24+4.24+24.4+4.4+24.24+24.24+24.24+24.24
= ( 24.24+24.24+24.24+24.24+24.24+24.24)+4.24+4.24+4.4
= 6(24.24)+24.8+4.4
= (6.24+6.24+24.8)+4.4
= 24.20+4.4
= 4.6.4.5+4.4
= 4.4(6.5+1)
= 16.(30+1)
= 16.31
16 tháng 5 2016
Ta có: 24.24+28.28+48.48
= 24.24+(24+4).(24+4)+(24+24).(24+24)
=24.24+24.24+4.24+24.4+4.4+24.24+24.24+24.24+24.24
= ( 24.24+24.24+24.24+24.24+24.24+24.24)+4.24+4.24+4.4
= 6(24.24)+24.8+4.4
= (6.24+6.24+24.8)+4.4
= 24.20+4.4
= 4.6.4.5+4.4
= 4.4(6.5+1)
= 16.(30+1)
= 16.31
c) \(4sin3x\cdot sin2x\cdot cosx=2(cosx-cos5x)\cdot cosx\)
\(=2cos^2x-2cos5x\cdot cosx\)
\(=2cos^2x-cos4x-cos6x\)
\(=1+cos2x-cos4x-cos6x\)
d) \(4sin\dfrac{13x}{2}\cdot cosx\cdot cos\dfrac{x}{2}=4sin\dfrac{x}{2}\cdot cos\dfrac{x}{2}\cdot cosx\)
\(=2sinx\cdot cosx\)
\(=sin2x\)