cho góc xoy=90o và Oz là phân giác của góc đó, từ A thuộc Oz kẻ AB vuông góc với Oz ( B thuộc Oz); kẻ AC vuông góc với Oy ( C thuộc Oy) lấy M thuộc AB, từ M kẻ MN sao cho góc NMO= góc BMO. CMR: góc MON = 45o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2021
a) Đề sai rồi bạn
b) Xét ΔOAB và ΔOCB có
OA=OC(gt)
\(\widehat{AOB}=\widehat{COB}\)(OB là tia phân giác của \(\widehat{AOC}\))
OB chung
Do đó: ΔOAB=ΔOCB(c-g-c)
Suy ra: AB=CB(hai cạnh tương ứng)
Ta có: OA=OC(gt)
nên O nằm trên đường trung trực của AC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=CB(cmt)
nên B nằm trên đường trung trực của AC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OB là đường trung trực của AC
hay OB\(\perp\)AC(đpcm)
10 tháng 4 2023
a: Xet ΔOAP vuông tại A và ΔOBP vuông tại B co
OP chung
góc AOP=góc BOP
=>ΔOAP=ΔOBP
=>OA=OB
=>ΔOAB cân tại O
b: ΔOAB cân tại O
mà OP là phân giác
nên OP vuông góc AB
SS
10 tháng 2 2022
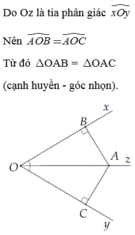
Vì Oz là tia phân giác của góc xOy
=>góc AOM = góc BOM
VÌ MA\(\perp\)Ox =>góc MAO=90o
MB \(\perp\)Oy =>góc MBO=90o
Xét \(\Delta AOM\)và \(\Delta BOM\)có:
Góc MAO= Góc MBO(Cùng bằng 90o)
OM:cạnh chung
Góc AOM = góc BOM
=>\(\Delta AOM=\Delta BOM\left(Ch-gn\right)\)
=>MA=MB(các cạnh tương ứng)