Cho d: y = -x + m, (P): \(y=x^2+\left(2-m\right)x-1\)và C(2;5). Tìm m để d cắt (P) tại hai điểm phân biệt là A và B sao cho tam giác ABC đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=2x-m\Leftrightarrow x^2-2x+m=0\) (*)
Pt (*) có \(\Delta'=\left(-1\right)^2-1.m=1-m\)
Để (d) cắt (P) tại 2 điểm phân biệt \(x_1,x_2\) thì pt (*) phải có 2 nghiệm phân biệt \(x_1,x_2\) \(\Leftrightarrow\Delta'>0\Leftrightarrow1-m>0\Leftrightarrow m< 1\)
Khi \(m< 1\), áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}y_1=x_1^2\\y_2=x_2^2\end{matrix}\right.\)\(\Rightarrow y_1+y_2=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=2^2-2m=4-2m\)
Do đó để \(y_1+y_2+x_1^2x_2^2=6\left(x_1+x_2\right)\)\(\Leftrightarrow4-2m+m^2=6.2\)\(\Leftrightarrow m^2-2m-8=0\) (1)
pt (1) có \(\Delta'=\left(-1\right)^2-1.\left(-8\right)=9>0\)
Vậy (1) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}m_1=\dfrac{-\left(-1\right)+\sqrt{9}}{1}=4\\m_2=\dfrac{-\left(-1\right)-\sqrt{9}}{1}=-2\end{matrix}\right.\)
Như vậy để (d) cắt (P) tại 2 điểm có hoành độ và tung độ thỏa mãn yêu cầu đề bài thì \(\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)
Mà do \(m< 1\) nên ta chỉ nhận trường hợp \(m=-2\)
Vậy để (d) cắt (P) tại 2 điểm phân biệt có hoành độ và tung độ thỏa mãn đề bài thì \(m=-2\)

a: Để (d1) và (d2) cắt nhau thì \(2m+1\ne m+2\)
=>\(2m-m\ne2-1\)
=>\(m\ne1\)
b: Khi m=-1 thì (d1): \(y=\left(2-1\right)x+1=x+1\)
Khi m=-1 thì (d2): \(y=\left(1-2\right)x+2=-x+2\)
Vẽ đồ thị:
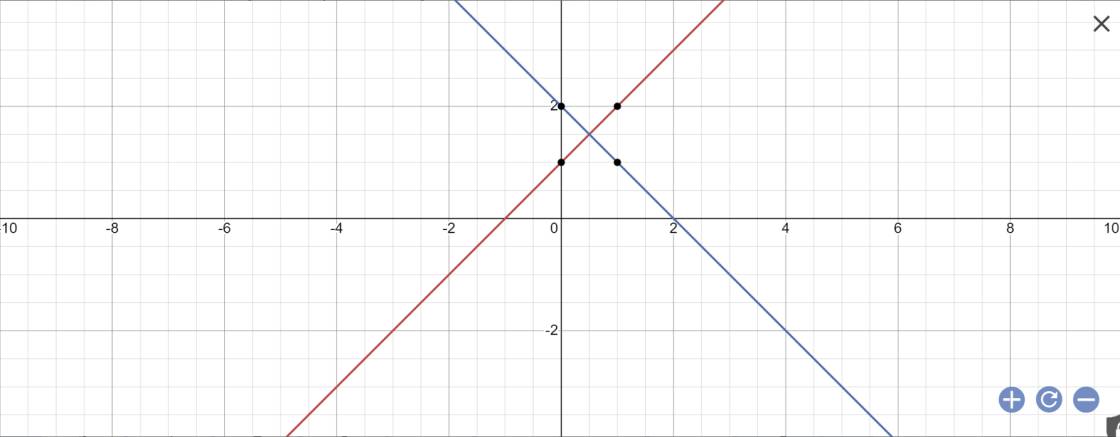
Phương trình hoành độ giao điểm là:
x+1=-x+2
=>x+x=2-1
=>2x=1
=>\(x=\dfrac{1}{2}\)
Thay x=1/2 vào y=x+1, ta được:
\(y=\dfrac{1}{2}+1=\dfrac{3}{2}\)
c:
(d1): y=(m+2)x+1
=>(m+2)x-y+1=0
Khoảng cách từ A(1;3) đến (d1) là:
\(d\left(A;\left(d1\right)\right)=\dfrac{\left|1\left(m+2\right)+3\cdot\left(-1\right)+1\right|}{\sqrt{\left(m+2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|m\right|}{\sqrt{\left(m+2\right)^2+1}}\)
Để d(A;(d1)) lớn nhất thì m+2=0
=>m=-2
Vậy: \(d\left(A;\left(d1\right)\right)_{max}=\dfrac{\left|-2\right|}{\sqrt{\left(-2+2\right)^2+1}}=\dfrac{2}{1}=2\)

\(\dfrac{1}{2}x^2-\left(-2+1\right)x+\dfrac{-2-1}{2}=0\)
\(\Rightarrow\dfrac{1}{2}x^2+x-\dfrac{3}{2}=0\)
Tới đây dùng \(\Delta\) chứ, nếu bn lấy \(\dfrac{1}{2}\) đặt lm nhân tử chung thì ở đây hơi vô lí

b: Phương trình hoành độ giao điểm là:
\(x^2-2\left(m-1\right)x-m^2-2m=0\)
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(-m^2-2m\right)\)
\(=4m^2-8m+4+4m^2+8m=8m^2+4>0\)
Vậy: Phương trình luôn có hai nghiệm phân biệt
\(x_1^2+x_2^2+4x_1x_2=36\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=36\)
\(\Leftrightarrow\left[2\left(m-1\right)\right]^2+2\left(-m^2-2m\right)=36\)
\(\Leftrightarrow4m^2-8m+4-2m^2-4m-36=0\)
\(\Leftrightarrow2m^2-12m-32=0\)
\(\Leftrightarrow\left(m-8\right)\left(m+2\right)=0\)
hay \(m\in\left\{8;-2\right\}\)

Gọi \(A\left(x_1;x_1^2\right)\) và \(B\left(x_2;x_2^2\right)\) là 2 điểm thuộc (P) và đối xứng qua M
Do A; B đối xứng qua M
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2.\left(-1\right)\\x_1^2+x_2^2=2.5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=-2-x_1\\x_1^2+x_2^2=10\end{matrix}\right.\)
\(\Rightarrow x_1^2+\left(-2-x_1\right)^2=10\)
\(\Rightarrow2x_1^2+4x_1-6=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-3\end{matrix}\right.\)
Vậy 2 điểm đó là \(\left(1;1\right)\) và \(\left(-3;9\right)\)

Phương trình hoành độ giao điểm là:
\(x^2-\left(2m+1\right)x+m^2-1=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\left(m^2-1\right)\)
\(=4m^2+4m+1-4m^2+4=4m+5\)
Để (P) cắt (d) tại hai điểm nằm về hai phía của trục tung thì \(m^2-1< 0\)
hay -1<m<1

gợi ý nè .
1) áp dụng bunya
2)thử nhân Pt 2 với 5 rồi trừ đi thử
3) đặt x3=a,y2=b
=> a2+3a+1=b2
đến đây có thể xét delta hoặc...
a2<a2+3a+1<a2+4a+4
=> a2<b2<(a+2)2
x,y nguyên nên a,b nguyên => b2=(a+1)2<=> a2+3a+1=a2+2a+1
<=> a=0 => b=1 => x=0 ,y=1

Bạn tham khảo:
Câu hỏi của Thiếu Niên Thần Thánh - Toán lớp 9 | Học trực tuyến