cho \(\Delta ABC\)cân tại \(\widehat{A}\),\(\widehat{A}\)=100 đọ , lấy điểm M \(\in\)AB \(N\in AC\). Sao cho AM=AN
chứng minh:
\(MN//BC\)
nhanh mình tích
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 6 2017
Ta có hình vẽ :
Ta có:
\(\Delta ABC\) cân tại A
=> \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-100^0}{2}=40^0\) ( hai góc đáy của tam giác cân ) (1)
Theo bài ra ta lại có:
AM=AN
=> \(\Delta AMN\) cân tại A ( trong tam giác có 2 góc bằng nhau )
\(\Rightarrow\widehat{AMN}=A\widehat{NM}=\dfrac{180^0-\widehat{A}}{2}=40^0\) ( hai góc đáy của tam giác cân) (2)
Từ (1) và (2) suy ra:\(\widehat{B}=\widehat{AMN}\)
=> MN//BC ( vì có cặp góc đồng vị )
(đ.p.c.m)
2T
2 tháng 9 2019
a) \(\Delta ABC\)cân tại A có \(\widehat{B}=\widehat{C}\)nên \(\widehat{A}=180^0-2.40^0=100^0\)
Vẽ \(DE//BC\left(E\in AB\right)\)
Trên tia BC lấy điểm F sao cho BD = BF.
Vì BD là phân giác của \(\widehat{B}\)nên \(\widehat{ABD}=\widehat{DBC}=\frac{\widehat{B}}{2}=20^0\)
Vì \(DE//BC\)nên \(\widehat{EDB}=\widehat{DBC}\)(so le trong)
Mà \(\widehat{ABD}=\widehat{DBC}\)(Do BD là phân giác của \(\widehat{B}\))
Suy ra \(\widehat{EDB}=\widehat{ABD}\)\(\Rightarrow\Delta EBD\)tại E \(\Leftrightarrow EB=ED\)(1)
Vì \(DE//BC\)nên \(\hept{\begin{cases}\widehat{AED}=\widehat{B}\\\widehat{ADE}=\widehat{C}\end{cases}}\)(đồng vị)
Mà \(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A) nên \(\widehat{AED}=\widehat{ADE}\)
\(\Rightarrow\Delta AED\)cân tại A \(\Rightarrow AE=AD\)
Lại có AB = AC (gt) nên EB = DC (2)
Từ (1) và (2) suy ra ED = DC
BD = BF(theo cách vẽ) nên \(\Delta BDF\)cân tại B có \(\widehat{DBF}=20^0\)
\(\Rightarrow\widehat{BDF}=\widehat{BFD}=\frac{180^0-20^0}{2}=80^0\)
Mà \(\widehat{DFB}+\widehat{DFC}=180^0\)(kề bù) nên \(\widehat{DFC}=180^0-80^0=100^0\)
Áp dụng định lý về tổng ba góc trong tam giác vào tam giác FDC, có:
\(\widehat{FDC}=180^0-100^0-40^0=40^0\)
Xét \(\Delta AED\)và \(\Delta FDC\)có:
\(\widehat{ADE}=\widehat{FCD}\left(=40^0\right)\)
ED = DC( cmt)
\(\widehat{AED}=\widehat{FDC}\left(=40^0\right)\)
Suy ra \(\Delta AED=\Delta FDC\left(g-c-g\right)\)
\(\Rightarrow AD=FC\)(hai cạnh tương ứng)
Lúc đó: \(BD+AD=BF+FC=BC\left(đpcm\right)\)
b) Vẽ tam giác đều AMG trên nửa mặt phẳng bờ AB chứa điểm C
Ta có: \(\widehat{GAC}=\widehat{BAC}-\widehat{BAG}=100^0-60^0=40^0\)
2 tháng 9 2019
Cách khác theo cô Huyền:3
Câu hỏi của thu - Toán lớp 7 - Học toán với OnlineMath
13 tháng 4 2020
Vì \(\Delta ABC\)là tam giác cân tại A
=> \(\widehat{B}=\widehat{C}\)( hai góc ở đáy )
=> \(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{80^0}{2}=40^0\)
Xét \(\Delta AMN\)có \(AM=AN\)
=> \(\Delta AMN\)là tam giác cân tại A
=> \(\widehat{M}_1=\widehat{N}\)( hai góc ở đáy )
Lại có : \(\widehat{M_1}+\widehat{N}=180^0-\widehat{A}=180^0-100^0=80^0\)
=> \(\widehat{M_1}=\widehat{N}=\frac{80^0}{2}=40^0\)
Ta có : \(\widehat{M_1}+\widehat{M_2}=180^0\)( kề bù )
=> \(\widehat{M_2}=180^0-\widehat{M_1}=180^0-40^0=140^0\)
Ta có : \(\widehat{B}+\widehat{M_2}=40^0+140^0=180^0\)( 1 )
mà \(\widehat{B}\)và \(\widehat{M_2}\)ở vị trí trong cùng phía ( 2 )
Từ ( 1 ) và ( 2 ) => \(MN//BC\)( đpcm )
18 tháng 9 2023
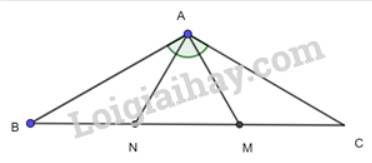
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.
12 tháng 9 2019
Vì tam giác ABC cân tại A nên \(\widehat{A}=\widehat{B}\)
\(\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\)
= \(\frac{180^o-100^o}{2}=40^o\) ( 1 )
Mà AM = AN ( gt ) nên \(\Delta AMN\) cân tại A \(\Rightarrow\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{AMN}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-100^o}{2}=40^o\) ( 2)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{B}=\widehat{AMN}\)
Vậy \(MN//BC\) ( vì có cặp góc ở vị trí đồng vị bằng nhau )
Chúc bạn học tốt !!!