Cho đoạn thẳng AB. Trên cùng nửa mặt phẳng bờ AB kẻ 2 tia Ax, By vuông góc với AB. Trên tia Ax và By lấy lần lượt 2 đỉểm C và D sao cho \(\widehat{COD}=90^o\) (O là trung điểm của AB). Chứng minh:
a, CD = AC + BD
b, CD là tiếp tuyến của đường tròn có đường kính AB
c, \(AC\cdot...
Đọc tiếp
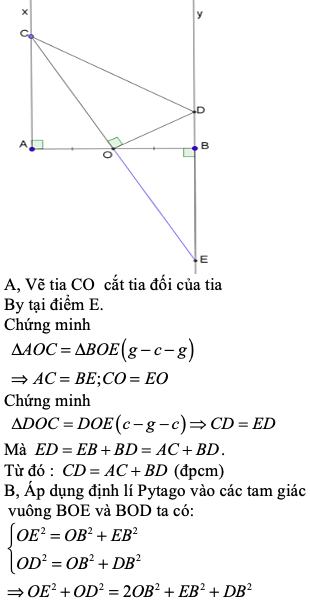
Cho đoạn thẳng AB. Trên cùng nửa mặt phẳng bờ AB kẻ 2 tia Ax, By vuông góc với AB. Trên tia Ax và By lấy lần lượt 2 đỉểm C và D sao cho \(\widehat{COD}=90^o\) (O là trung điểm của AB). Chứng minh:
a, CD = AC + BD
b, CD là tiếp tuyến của đường tròn có đường kính AB
c, \(AC\cdot BD=\dfrac{AB^2}{4}\)
Tự vẽ hình nha :) T làm ngắn gọn :)
a, Kéo dài OC cắt BD tại K
Kẻ OH vuông góc với CD (\(H\in CD\))
C/m: \(\Delta ACO=\Delta BKO\) (g.c.g)\(\Rightarrow AC=BK\)
\(\Rightarrow OC=OK\) \(\Rightarrow\Delta CDK\) cân tại D \(\Rightarrow DC=DK\) (1)
\(\Rightarrow\widehat{HCO}=\widehat{BKO}\)
\(\Rightarrow\Delta HCO=\Delta BKO\left(ch-gn\right)\)
\(\Rightarrow HC=BK\) (2) mà \(AC=BK\)
Từ (1), (2) \(\Rightarrow DH=BD\)
\(\Rightarrow AC+BD=DH+HC=CD\)
b, \(\Delta HCO=\Delta BKO\) (câu a)\(\Rightarrow OH=OB\)
H thuộc đường tròn tâm O mà OH vuông góc với CD
\(\Rightarrow\) CD là tiếp tuyến của đường tròn có đường kính AB
c,\(\Delta ACO\sim\Delta BOD\) (g.g)
\(\Rightarrow\dfrac{AC}{AO}=\dfrac{OB}{BD}\Rightarrow AC.BD=OA^2\)
Mà \(OA=\dfrac{AB}{2}\Rightarrow OA^2=\dfrac{AB^2}{4}\)
\(\Rightarrow AC.BD=\dfrac{AB^2}{4}\)