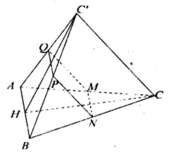
cho hai tam giác ABC và tam giác ABD , chung cạnh AB và hai đỉnh D và C nằm trong 2 mặt phẳng đối nhau , bờ là đường thẳng AB . Gọi M, N , P , Q theo thứ tự là các trung điểm các cạnh AC , CB , BD , AD
a / C/m MN // PQ vf MN = PQ
b/ Giả sử AB vuông góc DC . C/m MN vuông góc PN


a: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=AB/2
Xét ΔDAB có DQ/DA=DP/DB
nên QP//AB và QP=AB/2
=>MN//PQ và MN=PQ
b: Xét ΔBCD có BN/BC=BP/BD
nên NP//CD
=>NP vuông góc AB
=>NP vuông góc với MN