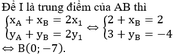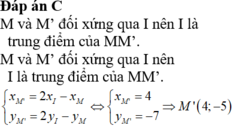Trong mặt phẳng tọa độ Oxy , cho điểm I(2;1). Tìm tọa độ các điểm A,B tương ứng thuộc các tia Ox, Oy sao cho tổng IA+IB+AB có độ dài nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Lời giải:
$I$ là trung điểm $AB$ nên:
\(\left\{\begin{matrix}
\frac{x_A+x_B}{2}=x_I\\
\frac{y_A+y_B}{2}=y_I\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x_B=2x_I-x_A\\
y_B=2y_I-y_A\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x_B=2.0-1=-1\\ y_B=2(-2)-0=-4\end{matrix}\right.\)
Vậy $B(-1,-4)$
CM
8 tháng 8 2019
Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C
AH
Akai Haruma
Giáo viên
28 tháng 10 2021
Lời giải:
Gọi $M'(a,b)$ là ảnh của $M$ qua phép vị tự $V,I$
a. Ta có:
\(\overrightarrow{OM'}=-2\overrightarrow{OM}\Leftrightarrow (a,b)=-2(2,1)=(-4,-2)\)
Vậy $M'(-4,-2)$
b. \(\overrightarrow{IM'}=4\overrightarrow{IM}\Leftrightarrow (a+1,b-3)=4(3, -2)\)
\(\Leftrightarrow \left\{\begin{matrix} a+1=4.3=12\\ b-3=4(-2)=-8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=11\\ b=-5\end{matrix}\right.\)
CM
16 tháng 2 2018
Đáp án C
Phương pháp: M và M’ đối xứng qua I nên I là trung điểm của MM’.
Cách giải: M và M’ đối xứng qua I nên I là trung điểm của MM’.
Ta có
CM
23 tháng 5 2017
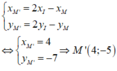
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
⇔ I M ' → = 5 I M → ⇔ x − 1 = 5 2 − 1 y − 2 = 5 − 3 − 2 ⇔ x = 6 y = − 23
Suy ra M’(6; -23).
Đáp án C
