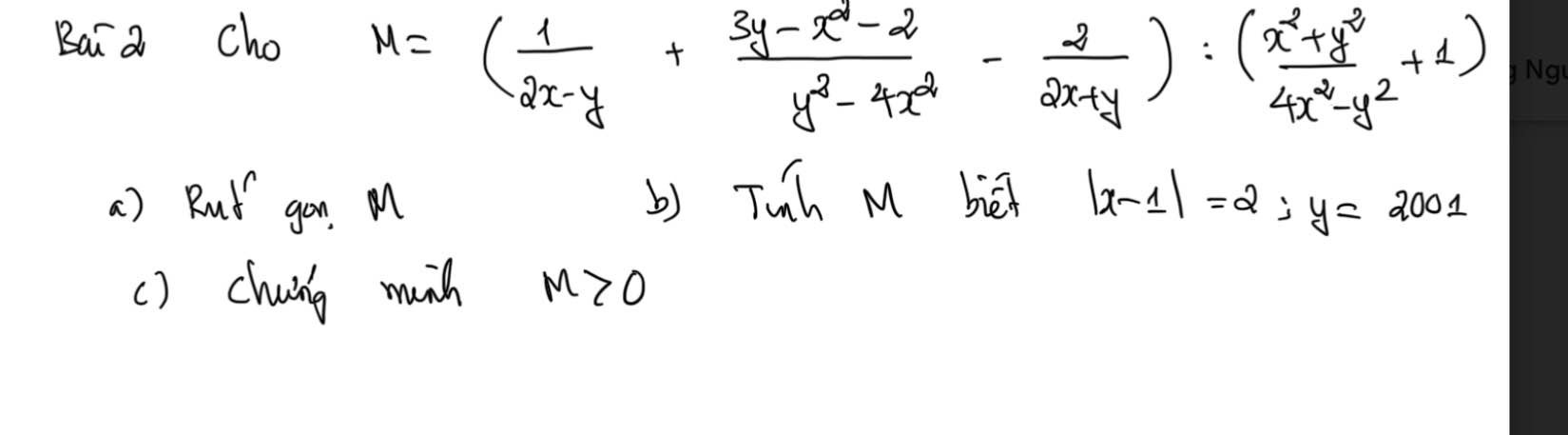Giúp mình câu a b c với ạ. Gấp lắm😓
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2022
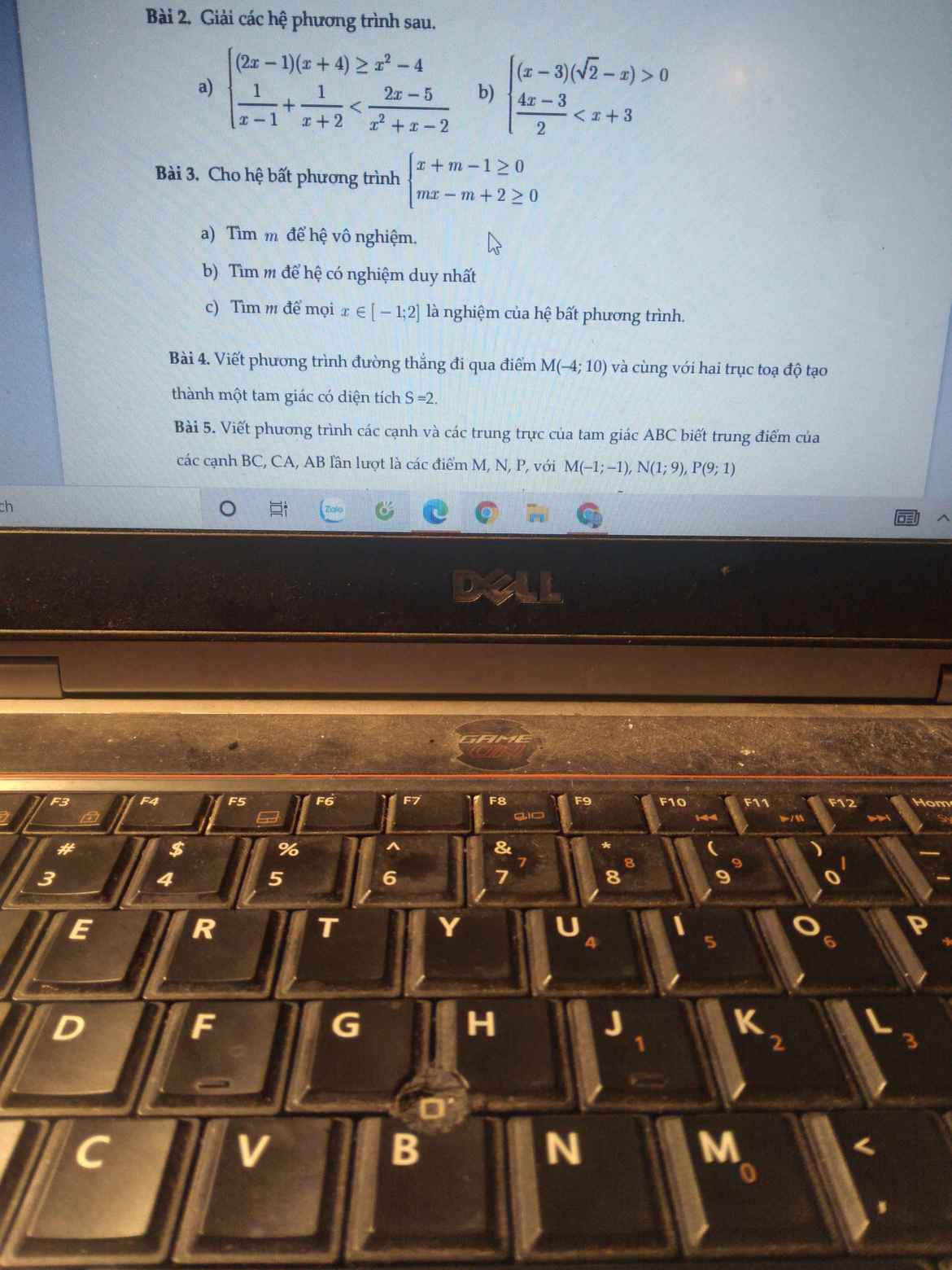
C3: Hệ bpt trở thành: \(\left\{{}\begin{matrix}x\ge1-m\\mx\ge2-m\end{matrix}\right.\)
a, Để hệ phương trình vô nghiệm thì \(m=0\)
b, Để hệ có nghiệm duy nhất thì \(\left\{{}\begin{matrix}m\ne0\\\dfrac{m-2}{m}=1-m\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m\ne0\\m=\pm\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(m=\pm\sqrt{2}\)
c, \(x\in\left[-1;2\right]\) \(\Leftrightarrow\) \(-1\le x\le2\)
Để mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt trên thì
\(\left\{{}\begin{matrix}-1\le1-m\le2\\-1\le\dfrac{2-m}{m}\le2\end{matrix}\right.\) với \(m\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2\ge m\ge-1\\m\ge\dfrac{2}{3}\end{matrix}\right.\) \(\left(m\ne0\right)\)
\(\Leftrightarrow\) \(2\ge m\ge\dfrac{2}{3}\)
Vậy \(m\in\left[\dfrac{2}{3};2\right]\) thì mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt
Chúc bn học tốt!
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2023
27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2023
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)
83
2
S
16 tháng 1 2022
PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
16 tháng 1 2022
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1 2022
Phương trình hoành độ giao điểm (d) và (P):
\(x^2-2x-3=ax-a-3\)
\(\Leftrightarrow x^2-\left(a+2\right)x+a=0\)
\(\Delta=\left(a+2\right)^2-4a=a^2+4>0;\forall a\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=a+2\\x_Ax_B=a\end{matrix}\right.\)
Mặt khác do A, B thuộc (d) nên: \(\left\{{}\begin{matrix}y_A=ax_A-a-3\\y_B=ax_B-a-3\end{matrix}\right.\)
\(y_A+y_B=0\)
\(\Leftrightarrow a\left(x_A+x_B\right)-2a-6=0\)
\(\Leftrightarrow a\left(a+2\right)-2a-6=0\)
\(\Leftrightarrow a^2-6=0\)
\(\Leftrightarrow a=\pm\sqrt{6}\)
21 tháng 9 2021
a: Ta có: \(M=\left(\dfrac{1}{2x-y}-\dfrac{-x^2+3y-2}{4x^2-y^2}-\dfrac{2}{2x+y}\right):\left(\dfrac{x^2+y^2}{4x^2-y^2}+1\right)\)
\(=\dfrac{2x+y+x^2-3y+2-4x+2y}{\left(2x-y\right)\left(2x+y\right)}:\dfrac{x^2+y^2+4x^2-y^2}{\left(2x-y\right)\left(2x+y\right)}\)
\(=\dfrac{x^2-2x+2}{5x^2}\)
c: Ta có: \(\left\{{}\begin{matrix}x^2-2x+2=\left(x-1\right)^2+1>0\forall x\\5x^2>0\forall xtmĐKXĐ\end{matrix}\right.\)
Do đó: M>0
NT
0
17 tháng 1 2022
Câu 16.
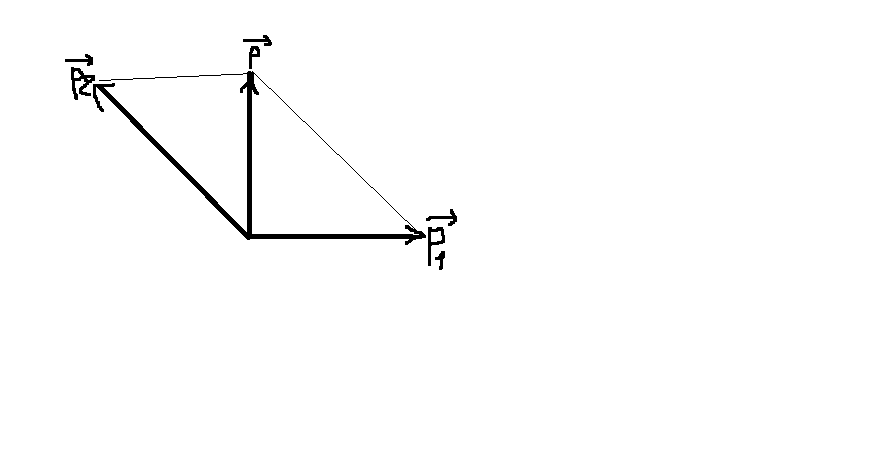
Hình vẽ tương đối thôi nha!!!
Bảo toàn động lương ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_2^2-p_1^2\)\(\Rightarrow p_2=\sqrt{p^2+p_1^2}\)
\(\Rightarrow m_2\cdot v_2=\sqrt{\left(m_1+m_2\right)\cdot v+m_1\cdot v_1}\)
\(\Rightarrow0,3\cdot v_2=\sqrt{[\left(0,5+0,3\right)\cdot3]^2+(0,5\cdot4)^2}=3,124\)
\(\Rightarrow v_2=10,41\)m/s