Cho tứ giác ABCD có 2 đường chéo AC và BD vuông góc với nhau.Gọi M ; N ; I ; K lần lượt là trung điểm AB ;BC; CD ;DA.
a,Chứng minh tứ giác MNIK là hình bình hành
b,Chứng minh tứ giác MNIK là hình chữ nhật
c,Chứng minh MI = MK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
11 tháng 10 2020
Ta có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của ∆ABD => MN // BD
Mà AC⊥BD nên MN⊥AC hay LA⊥MN (1)
N, L lần lượt là trung điểm của AD, AC nên NL là đường trung bình của ∆ADC => NL // DC
Mà MH⊥DC nên NL⊥MH (2)
Từ (1) và (2) suy ra H là trực tâm của tam giác MNL (đpcm)
10 tháng 12 2016
tgiác ABC có MN là đường trung bình => MN // AC và MN = AC/2
tgiác DAC có PQ là đường trung bình => PQ // AC và PQ = AC/2
vậy: MN // PQ và MN = PQ => MNPQ là hình bình hành
mặt khác xét tương tự cho hai tgiác ABD và CBD ta cũng có:
NP // BD và NP = BD/2
do giả thiết AC_|_BD => AC_|_NP mà MN // AC => MN_|_NP
tóm lại MNPQ là hình chữ nhật (hbh có một góc vuông)
b) MNPQ là hình vuông <=> MN = NP <=> AC/2 = BD/2 <=> AC = BD
vậy điều kiện là: tứ giác ABCD có hai đường chéo vuông góc và bằng nhau
c, Vỳ Mn là đườq trung bình của tam giác ABC nên MN= \(\frac{1}{2}\) AC= 3cm
QM là đường trung bình của tam giác ABD nên QM = \(\frac{1}{2}\) BD = 4cm
Mà MNPQ là hình chữ nhật nên diện tích ABCD = ( MN+PQ).2= (3.4):2 = 6cm
11 tháng 12 2016
Bạn ơi lẽ ra chỗ diện tích hcn là phải bằng = 3 . 4 = 12cm chứ nhỉ bạn
8 tháng 11 2023
Xét ΔABD có
M,Q lần lượt là trung điểm của AB,AD
=>MQ là đường trung bình của ΔABD
=>MQ//BD và MQ=BD/2(1)
Xét ΔCBD có
N,P lần lượt là trung điểm của CB,CD
=>NP là đường trung bình của ΔCBD
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
Xét ΔBAC có
M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình
=>MN//AC
MN//AC
AC\(\perp\)BD
Do đó: MN\(\perp\)BD
MN\(\perp\)BD
MQ//BD
Do đó: MN\(\perp\)MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
Do đó: MNPQ là hình bình hành
Hình bình hành MNPQ có \(\widehat{NMQ}=90^0\)
nên MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn
CM
23 tháng 3 2018
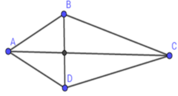
Vì ABCD có đường chéo vuông góc nên
SABCD = 1 2 BD. AC
=> AC = 2 S A B C D B D = 2.56 7 = 16 cm.
Đáp án cần chọn là: D
CM
27 tháng 5 2019
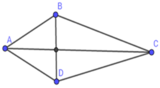
SABCD = 1 2 BD. AC
=> AC = 2 S A B C D B D = 2.25 5 = 10 cm.
Đáp án cần chọn là: A
a: Xét ΔABD có
M là trung điểm của AB
K là trung điểm của AD
Do đó: MK là đường trung bình của ΔBAD
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\left(1\right)\)
Xét ΔCBD có
N là trung điểm của BC
I là trung điểm của CD
Do đó: NI là đường trung bình của ΔCBD
Suy ra: NI//BD và \(NI=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MK//NI và MK=NI
hay MKIN là hình bình hành