Một chiếc thuyền đang hướng đến ngọn hải đăng cao 63m. Thuyền trưởng đo được góc nâng từ mặt nước đến đỉnh tháp là 19 độ. Mười phút sau, thuyền trưởng đo lại thì góc nâng lúc này là 54 độ. Hỏi thuyền đã đi được bao xa trong 10p đó?( làm tròn đến hàng đơn vị)Một chiếc thuyền đang hướng đến ngọn hải đăng cao 63m. Thuyền trưởng đo được góc nâng từ mặt nước đến đỉnh tháp là 19 độ. Mười phút sau, thuyền trưởng đo lại thì góc nâng lúc này là 54 độ. Hỏi thuyền đã đi được bao xa trong 10p đó?( làm tròn đến hàng đơn vị)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

11 tháng 12 2023
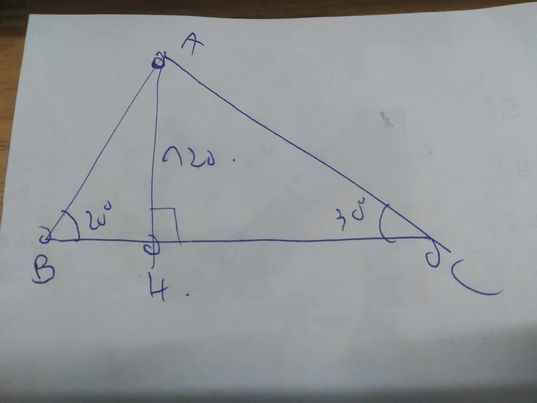
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát


B: Là vị trí thuyền hiện tại
D: là vị trí thuyền sau 10 phút
AC: chiều cao ngọn hải đăng = 63 m
Xét tg vuông ABC
\(\tan\widehat{ABC}=\tan19^o=\frac{AC}{AB}=\frac{63}{AB}\Rightarrow AB=\frac{63}{\tan19^o}\)
Xét tg vuông ACD có
\(\tan\widehat{ADC}=\tan54^o=\frac{AC}{AD}=\frac{63}{AD}\Rightarrow AD=\frac{63}{\tan54^o}\)
Quãng đường thuyền đi được sau 10' là
\(BD=AB-AD=\frac{63}{\tan19^o}-\frac{63}{\tan54^o}\)