K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
Kẻ Az//xx'(Az cùng phía Cx' trên nửa mp bờ AC)
\(\Rightarrow\)Az//yy'
\(\Rightarrow\widehat{CAz}=\widehat{ACx}=45^0\) (so le trong)\(;\widehat{zAD}=180^0-\widehat{ADy'}=72^0\)(trong cùng phía)
\(\Rightarrow\widehat{CAD}=\widehat{CAz}+\widehat{zAD}=117^0\)
17 tháng 10 2021
bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2
Y
23 tháng 2 2023
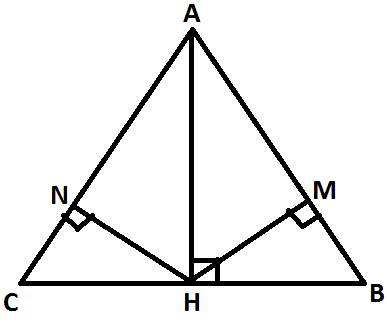
Ta có \(MN\perp AC\Rightarrow\) Tam giác AHC vuông tại H ; Tam giác AHB vuông tại H
Do \(\widehat{A_1}=\widehat{A_2}\) , \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
Suy ra được 2 góc còn lại của 2 tam giác bằng nhau
\(a,\) Xét \(\Delta AHC\) và \(\Delta AHB:\)
Có 3 góc trong tam giác đều bằng nhau \(\Rightarrow\Delta AHC=\Delta AHB\left(g-g-g\right)\)
\(b,\) \(\widehat{A_1}=\widehat{A_2}\Rightarrow\) A là đường phân giác của tam giác ABC\(\Rightarrow HC=HB\)
Xét \(\Delta HNC\) và \(\Delta HMB:\)
Có 2 góc bằng nhau \(\widehat{M}=\widehat{N}\left(=90^o\right);\widehat{C}=\widehat{B}\left(cmt\right)\)
Và \(HC=HB\left(cmt\right)\)
\(\Rightarrow\Delta HNC=\Delta HMB\left(g-c-g\right)\)
NT
3
17 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`(8x-3)(3x+2)-(4x+7)(x+4)=(2x+1)(5x-1)-33`
`\Leftrightarrow 8x(3x+2) -3(3x+2) - 4x(x+4) + 7(x+4) = 2x(5x-1) + 5x-1 - 33`
`\Leftrightarrow 24x^2 + 16x - 9x - 6 - 4x^2 - 16x - 7x - 28 = 10x^2 - 2x + 5x - 1 - 33`
`\Leftrightarrow 20x^2 -16x - 34 = 10x^2 + 3x - 34`
`\Leftrightarrow 20x^2 - 16x - 34 - 10x^2 - 3x + 34 = 0`
`\Leftrightarrow 10x^2 - 19x = 0`
`\Leftrightarrow x(10x - 19)=0`
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\10x-19=0\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\10x=19\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\x=\dfrac{19}{10}\end{matrix}\right.\)
Vậy, `x={0; 19/10}.`
8 tháng 7 2017
Ta có
3344=(3.11)44=344.1144=(34)11.1144=8111.1144
4433=(4.11)33=433.1133=(43)11.1133=6411.1133
=> 3344>4433
KL:
b) 52222=(52)1111=251111
25555=(25)1111=321111
=> 52222<25555
KL
Giúp mình với ạ mình cảm ơn:33
23 tháng 1 2022
Bài 4:
a: \(C=\left(\dfrac{1}{3}-\dfrac{1}{2}\right)x^3-2x^2-\left(4+1\right)x+1\)
\(=\dfrac{-1}{6}x^3-2x^2-5x+1\)
b: Thay x=2 vào C, ta được:
\(C=\dfrac{-1}{6}\cdot8-2\cdot4-5\cdot2+1=\dfrac{-4}{3}-8-10+1=\dfrac{-4}{3}-17=\dfrac{-4-51}{3}=-\dfrac{55}{3}\)
Bài 5:
Theo đề, ta có: \(\left(xyz\right)^2=2\cdot6\cdot3=36\)
Trường hợp 1: xyz=6
\(\Leftrightarrow\left\{{}\begin{matrix}z=3\\x=1\\y=2\end{matrix}\right.\)
Trường hợp 2: xyz=-6
\(\Leftrightarrow\left\{{}\begin{matrix}z=-3\\x=-1\\y=-2\end{matrix}\right.\)
HN
2
29 tháng 3 2021
a) Xét (O) có
\(\widehat{PFE}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{PFE}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{PFN}=90^0\)
Xét tứ giác PFMN có
\(\widehat{PFN}\) và \(\widehat{PMN}\) là hai góc cùng nhìn cạnh PN
\(\widehat{PFN}=\widehat{PMN}\left(=90^0\right)\)
Do đó: PFMN là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
27 tháng 9 2021
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^0\)
\(\widehat{ABC}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{AB}\Rightarrow AB^2=BC.BH\)
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ACB}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\Rightarrow AC^2=BC.HC\)
c) Ta có: \(\left\{{}\begin{matrix}\Delta ABC\sim\Delta HBA\left(cmt\right)\\\Delta ABC\sim\Delta HAC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\Rightarrow AH^2=CH.BH\)
d) Ta có: \(\Delta ABC\sim\Delta HAC\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AH}=\dfrac{BC}{AC}\Rightarrow AB.AC=BC.AH\)
KY
29 tháng 12 2021
gatherings - lucky - Before - always - clean - decorate - and - water
Yes, it is.
They can visit some famous places such as Tra Co Communal House, Linh Khanh Pagoda, and Tra Co Church.
They can find seafood from fishing boats.
They can take part in the festival from May 30 to June 6.
has a sofa.
we go to the cinema?
noisier than the countryside.
behave well at Tet.
29 tháng 12 2021
VII
25 gathering
26 lucky
27 Berofe
28 always
29 clean
30 decorate
31 and
32 water