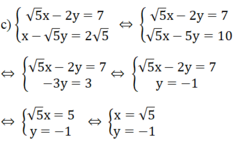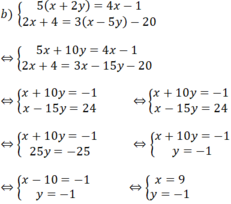giải các hệ phương trình sau
.{ 3xy = 5
{ 5x + 2y = 23
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=10\\5x+2y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=33\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\\15+2y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
\(\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-6x+2y=-10\\5x+2y=23\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\11x=33\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}5x+15y=-10\\5x-4y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-21\\5x-4y=11\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{21}{19}\\5x-4\left(-\dfrac{21}{19}\right)=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{19}\\y=-\dfrac{21}{19}\end{matrix}\right.\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\10x-5y=-40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\13x=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=2\end{matrix}\right.\\ d,\Leftrightarrow\left\{{}\begin{matrix}5x-10y=-30\\5x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-3y=5\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\\ e,\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+3\cdot6=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}9x^2-3xy+2y^2=23\\7x^2+6xy-8y^2=-37\end{matrix}\right.\)\(\left(hpt\right)\)
\(đặt:x=t.y\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}9\left(t.y\right)^2-3t.y^2+2y^2=23\left(1\right)\\7\left(ty\right)^2+6t.y^2-8y^2=-37\left(2\right)\end{matrix}\right.\)
\(\Rightarrow-37\left[9\left(t.y\right)^2-3ty^2+2y^2\right]=23\left[7\left(ty\right)^2+6ty^2-8y^2\right]\)
\(\Leftrightarrow494\left(ty\right)^2+27ty^2-110y^2=0\left(3\right)\)
\(x=y=0\) \(không\) \(là\) \(nghiệm\) \(hpt\)
\(y\ne0\Rightarrow\left(3\right)\Leftrightarrow494t^2+27t-110=0\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{110}{247}\Rightarrow x=\dfrac{110}{247}.y\left(4\right)\\t=-\dfrac{1}{2}\Rightarrow x=-\dfrac{1}{2}.y\left(5\right)\end{matrix}\right.\)
\(thay\left(4\right)và\left(5\right)vào-hpt\Rightarrow x,y=.....\)(đến đây dễ rồi bạn tự tìm x,y)

Cách 1
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
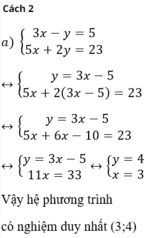

(Các phần giải thích học sinh không phải trình bày).
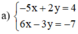 (Nhân 2 vế pt 1 với 3; nhân pt 2 với 2 để hệ số của y đối nhau)
(Nhân 2 vế pt 1 với 3; nhân pt 2 với 2 để hệ số của y đối nhau)
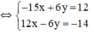 (hệ số của y đối nhau nên ta cộng từ vế 2 pt)
(hệ số của y đối nhau nên ta cộng từ vế 2 pt)
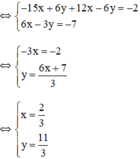
Vậy hệ phương trình có nghiệm duy nhất 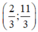

a ) \(\begin{cases}3x-y=5\\5x+2y=23\end{cases}\)
Từ phương trình \(\left(1\right)\) \(\Leftrightarrow y=3x-5\) \(\left(3\right)\)
Thế \(\left(3\right)\) vào phương trình \(\left(2\right)\) : \(5x+2\left(3x-5\right)=23\)
\(\Leftrightarrow5x+6x-10=23\Leftrightarrow11x=33\Leftrightarrow x=3\)
Từ đó \(y=3.3-5=4\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(3;4\right)\)
b ) \(\begin{cases}3x+5y=1\\2x-y=-8\end{cases}\)
Từ hệ phương trình \(\left(2\right)\) \(\Leftrightarrow y=3x+8\)
Thế (3) vào (1): \(3x+5\left(2x+8\right)=1\Leftrightarrow3x+10x+40=1\Leftrightarrow13x=-39\)
\(\Leftrightarrow x=-3\)
Từ đó \(y=2\left(-3\right)+8=2\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(-3;2\right)\)