Cho hai điện trở R1=R2=60w được mắc vào 2 điểm a,b. Nếu R1 mắc song song R2 thì điện trở R'AB của đoạn mạch khi đo là bao nhiêu?
A. R'AB=240w
B. R'AB=30w
C. R'AB=120w
D. R'AB=360w
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, gọi R1 R2 lần lượt là x1 x2 ta có
khi x1 nt x2 ta có x1+x2=90 (1)
khi x1 // x2 ta có \(\dfrac{x_1.x_2}{x_1+x_2}.4,5=90\Rightarrow\dfrac{x_1.x_2}{x_1+x_2}=20\Rightarrow x_1.x_2=1800\) (2)
từ (1) (2) \(\Rightarrow\left\{{}\begin{matrix}x_1=30\\x_1=60\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=60\\x_2=30\end{matrix}\right.\)

Khi R 1 mắc song song với R 2 thì:
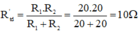
Vậy R ' t đ nhỏ hơn mỗi điện trở thành phần.

gọi R1,R2 lần lượt là x,y(ôm)
->hệ pt: \(\left\{{}\begin{matrix}x+y=100\\\dfrac{xy}{x+y}=16\end{matrix}\right.< =>\left\{{}\begin{matrix}y=100-x\left(1\right)\\\dfrac{x\left(100-x\right)}{x+100-x}=16\left(2\right)\end{matrix}\right.\)
giải pt(2)
\(=>\dfrac{100x-x^2}{100}=16< =>-x^2+100x-1600=0\)
\(\Delta=100^2-4\left(-1600\right)\left(-1\right)=3600>0\)
\(=>\left[{}\begin{matrix}x1=\dfrac{-100+60}{-2}=20\\x2=\dfrac{-100-60}{-2}=80\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y1=80\\y2=20\end{matrix}\right.\)
vậy (R1;R2)={(20;80),(80;20)}

– Công thức cần sử dụng:
Đối với đoạn mạch mắc nối tiếp: R t đ = R 1 + R 2
Đối với đoạn mạch mắc song song:
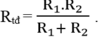
Khi R 1 nt R 2 ta có: R n t = R 1 + R 2 = 9 Ω ( 1 )
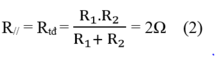
\(R_{AB}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.60}{60+60}=30\left(\Omega\right)\)
=>B
B