Vì sao B// Cy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NB
Nguyễn Bá Tú
27 tháng 9 2021
B chỉ là một điểm làm sao song song được
Đúng(0)
Những câu hỏi liên quan
31 tháng 10 2023
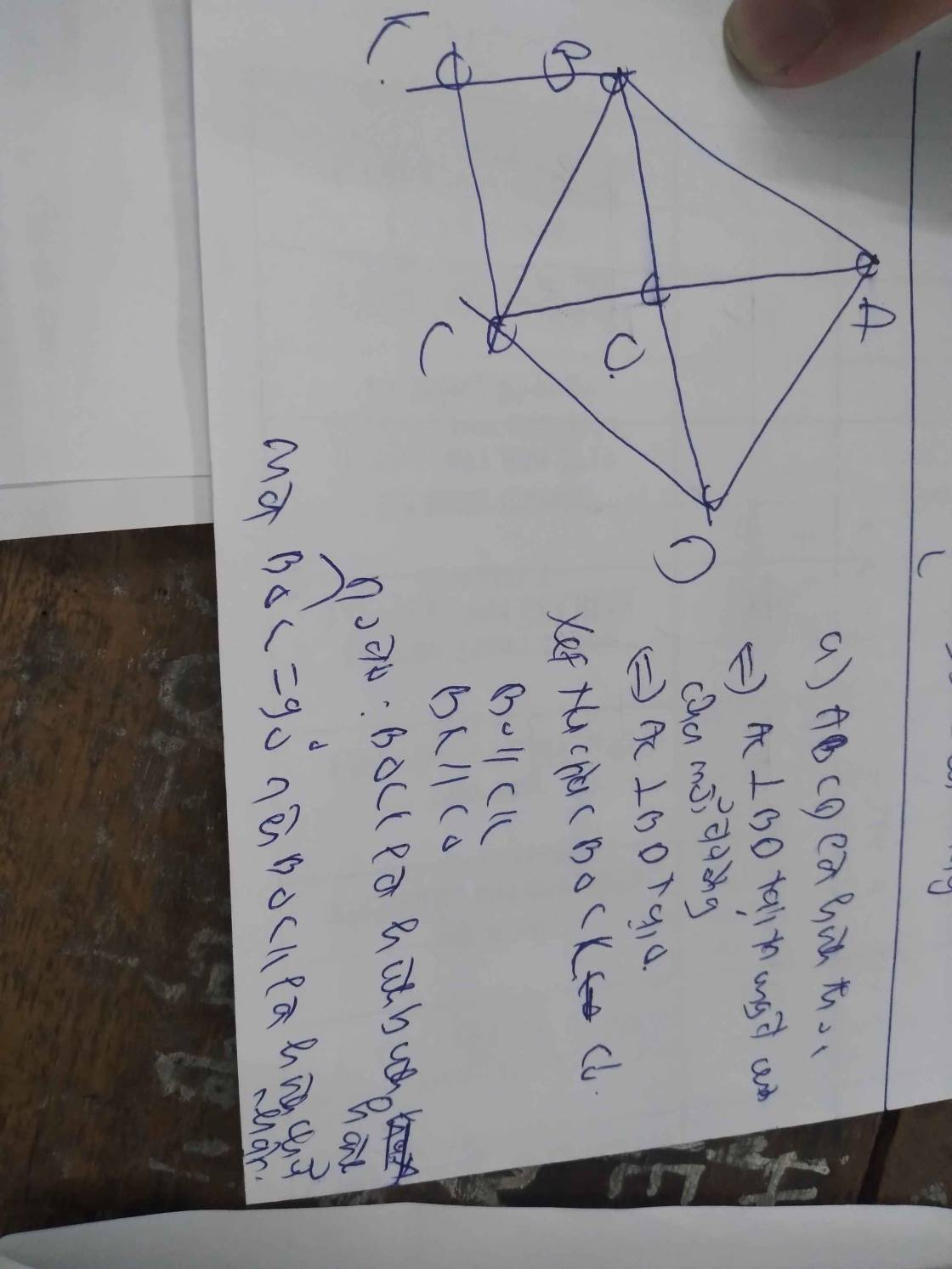
a) Tứ giác BOCK là tứ giác cân.
Để chứng minh điều này, ta cần chứng minh hai cặp góc của tứ giác BOCK bằng nhau.
Góc BOC và góc BKC là hai góc đối nhau nằm ở cùng một cạnh BC, nên chúng bằng nhau:
Góc BOC = Góc BKC. Góc BCO và góc BCK là hai góc đối nhau nằm ở cùng một cạnh BC, nên chúng bằng nhau: Góc BCO = Góc BCK.
Vì vậy, tứ giác BOCK có hai cặp góc bằng nhau, tức là tứ giác BOCK là tứ giác cân.
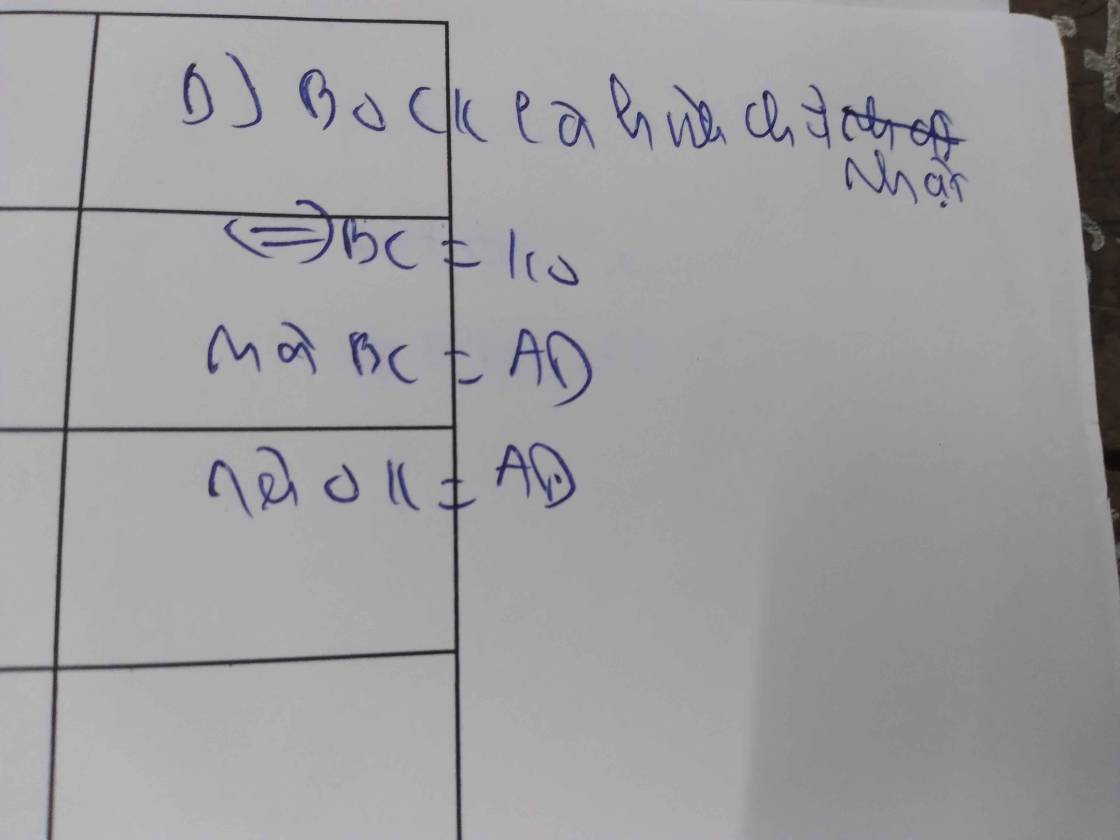
b) Ta cần chứng minh CM : OK = AD.
Vì tứ giác BOCK là tứ giác cân, nên ta có BC = BK.
Do đó, tam giác BCK là tam giác cân, nên ta có CM là đường trung tuyến của tam giác BCK.
Vì vậy, ta có CM = MK.
Từ đó, ta có CM : OK = MK : OK = 1 : 1 = 1.Tuy nhiên, để chứng minh CM : OK = AD, ta cần thêm thông tin về mối quan hệ giữa các đoạn thẳng trong hình thoi ABCD.
CM
11 tháng 1 2017
a) Các tia trùng với tia By là: tia BA và tia BC.
b) Hai tia Bx và Cy không trùng nhau, vì hai tia Bx và Cy không chung gốc.
20 tháng 5 2022
Tham khảo
a)
Ta có :
AB = OB - OA ( Vì A nằm giữa hai điểm O và B )
= 6cm - 4cm
= 2cm
OC = OB - BC ( Vì C nằm giữa hai điểm O và B )
= 6cm - 4cm
= 2cm
b)
Điểm A là trung điểm của đoạn thẳng BC vì điểm A chia đoạn thẳng BC thành 2 đoạn thẳng nhỏ bằng nhau
c)
- Góc nhọn : góc xCy
- Góc tù : góc zCy
- Góc bẹt : góc zCx
4 tháng 5 2022
giải thích các bước giải:
a.Ta có: OA<OBOA<OB
A,BA,B thuộc tia OxOx
→A→A nằm giữa O,BO,B
→AB=OB−OA=2(cm)→AB=OB−OA=2(cm)
Ta có: BC<BOBC<BO
C,O∈C,O∈ tia BABA
→C→C nằm giữa O,BO,B
→OC=OB−BC=2(cm)→OC=OB−BC=2(cm)
b.Ta có: OC<OA→COC<OA→C nằm giữa O,AO,A
→CA=OA−OC=2(cm)→CA=OA−OC=2(cm)
→OC=CA=12OA→OC=CA=12OA
→C→C là trung điểm OAOA
c.Góc nhọn là ˆxCy,ˆOCzxCy^,OCz^
Góc tù ˆOCy,ˆxCzOCy^,xCz^
Góc bẹt ˆOCx,ˆyOz,ˆOAx,ˆOBx