Cho 1/2 (O) đường kính AB . Trên cùng một nửa mặt phẳng bờ AB kẻ tiếp tuyến Ax , By của (O) , lấy điểm m thuộc nửa đường tròn , I thuộc AB sao cho AI < IB . Kẻ đường thẳng d vuông góc với MI tại M cắt Ax , By tại E và F .
a, CMR: tứ giác AEIM , MIBF nội tiếp
b, CMR: góc EIF = 90o
c, Tính AE . BF theo R
d,Tìm GTNN của SEIF theo R , dấu ''='' xảy ra khi nào ?

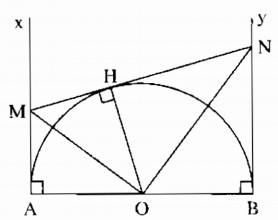


Sửa đề : I là trung điểm AO
a,Xét tứ giác AEIM có ^EAI + ^EMI = 90o
=> Tứ giác AEIM nội tiếp
Tương tự tứ giác MIBF nội tiếp
b,Vì tứ giác AEIM nội tiếp
=> ^MEI = ^MAI
Tương tự ^MFI = ^MBI
Vì M thuộc (O) đường kính AB
=> ^AMB = 90o
=> ^MAI + ^MBI = 90o
=> ^MEI + ^MFI = 90o
=> ^EIF = 90o
c, Xét \(\Delta\)AEI và \(\Delta\)BIF có
^EAI = ^FBI ( = 90o )
^AEI = ^BIF (Cùng phụ ^EIA)
\(\Rightarrow\Delta AEI\approx\Delta BIF\left(g.g\right)\)
=> AE . BF = AI . BI
Vì I là trung điểm AO
=> \(AI=\frac{AO}{2}=\frac{R}{2}\)
=> \(BI=AB-AI=2R-\frac{R}{2}=\frac{3R}{2}\)
\(\Rightarrow AE.BF=AI.BI=\frac{R}{2}.\frac{3R}{2}=\frac{3R^2}{4}\)
d,(Mấy cái lặt vặt tính cạnh theo R mình không làm nữa nhé , bạn tự hiểu nha)
Có \(S_{EIF}=S_{AEBF}-S_{AEI}-S_{BIF}\)
\(=\frac{\left(AE+BF\right).AB}{2}-\frac{AE.AI}{2}-\frac{BI.BF}{2}\)
\(=\frac{\left(AE+BF\right).2R}{2}-\frac{AE}{2}.\frac{R}{2}-\frac{BF}{2}.\frac{3R}{2}\)
\(=\left(AE+BF\right).R-\frac{AE.R}{4}-\frac{3BF.R}{4}\)
\(=AE.R-\frac{AE.R}{4}+BF.R-\frac{3BF.R}{4}\)
\(=\frac{3AE.R}{4}+\frac{BF.R}{4}\)
\(\ge2\sqrt{\frac{3AE.R.BF.R}{4.4}}\)
\(=2\sqrt{\frac{3R^2.AE.BF}{16}}\)
\(=2\sqrt{\frac{3R^2.\frac{3R^2}{4}}{16}}\)
\(=\frac{3R^2}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{3AE.R}{4}=\frac{BF.R}{4}\)
\(\Leftrightarrow3AE=BF\)
Thay vào \(AE.BF=\frac{3R^2}{4}\)
\(\Leftrightarrow AE.3AE=\frac{3R^2}{4}\)
\(\Leftrightarrow AE=\frac{R}{2}\)
\(\Leftrightarrow BF=\frac{3R}{2}\)
Vậy .,..........