điều kiện của phân thức 1/(a+b+c)^2-3(ab+bc+ac)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề ra, ta có:
\(a^2+b^2+c^2\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2\right)\)
\(=a^3+b^3+c^3+a^2b+b^2c+c^2a+ab^2+bc^2+ca^2\)
Theo BĐT Cô-si:
\(\left\{{}\begin{matrix}a^3+ab^2\ge2a^2b\\b^3+bc^2\ge2b^2c\\c^3+ca^2\ge2c^2a\end{matrix}\right.\Rightarrow a^2+b^2+c^2\ge3\left(a^2b+b^2c+c^2a\right)\)
Do vậy \(M\ge14\left(a^2+b^2+c^2\right)+\dfrac{3\left(ab+bc+ac\right)}{a^2+b^2+c^2}\)
Ta đặt \(a^2+b^2+c^2=k\)
Luôn có \(3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2=1\)
Vì thế nên \(k\ge\dfrac{1}{3}\)
Khi đấy:
\(M\ge14k+\dfrac{3\left(1-k\right)}{2k}=\dfrac{k}{2}+\dfrac{27k}{2}+\dfrac{3}{2k}-\dfrac{3}{2}\ge\dfrac{1}{3}.\dfrac{1}{2}+2\sqrt{\dfrac{27k}{2}.\dfrac{3}{2k}}-\dfrac{3}{2}=\dfrac{23}{3}\)
\(\Rightarrow Min_M=\dfrac{23}{3}\Leftrightarrow a=b=c=\dfrac{1}{3}\).

`1)(a+b+c)^2=3(a^2+b^2+c^2)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3a^2+3b^2+3c^2`
`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`
`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`
`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`
Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`
Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`
`2)(a+b+c)^2=3(ab+bc+ca)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca`
`<=>a^2+b^2+c^2=ab+bc+ca`
`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`
`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`
`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`
Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`
Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`
Vậy nếu `a=b=c` thì ....

\(P=\frac{a^3b^2c^2}{ab+a^2bc+abc}+\frac{ab^2c}{bc+b+abc}+\frac{abc^2}{ac+c+1}\)
\(=\frac{ }{ab\left(1+ac+c\right)}+\frac{ }{b\left(c+1+ac\right)}+\frac{ }{ac+c+1}\)

\(Q=\left(a^2b^2+a^2+b^2+1\right)\left(c^2+1\right)=\)
\(=a^2b^2c^2+a^2b^2+a^2c^2+a^2+b^2c^2+b^2+c^2+1=\)
\(=a^2b^2c^2+\left(a^2b^2+b^2c^2+a^2c^2\right)+\left(a^2+b^2+c^2\right)+1\) (1)
Ta có
\(\left(ab+bc+ac\right)^2=a^2b^2+b^2c^2+a^2c^2+2ab^2c+2abc^2+2a^2bc=\)
\(=a^2b^2+b^2c^2+a^2c^2+2abc\left(a+b+c\right)=1\)
\(\Rightarrow a^2b^2+b^2c^2+a^2c^2=1-2abc\left(a+b+c\right)\) (2)
Ta có
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ac\right)=\)
\(=a^2+b^2+c^2+2\)
\(\Rightarrow a^2+b^2+c^2=\left(a+b+c\right)^2-2\) (3)
Thay (2) và (3) vào (1)
\(Q=a^2b^2c^2+1-2abc\left(a+b+c\right)+\left(a+b+c\right)^2-2+1=\)
\(=\left(abc\right)^2-2abc\left(a+b+c\right)+\left(a+b+c\right)^2=\)
\(=\left[abc-\left(a+b+c\right)\right]^2\)

\(a,\dfrac{3}{a+b}=\dfrac{2}{b+c}=\dfrac{1}{c+a}\\ \Rightarrow\dfrac{a+b}{3}=\dfrac{b+c}{2}=\dfrac{c+a}{1}=\dfrac{2\left(a+b+c\right)}{6}=\dfrac{a+b+c}{3}\\ \Rightarrow\dfrac{a+b}{3}=\dfrac{a+b+c}{3}\\ \Rightarrow3\left(a+b+c\right)=3\left(a+b\right)\\ \Rightarrow3\left(a+b\right)+3c=3\left(a+b\right)\\ \Rightarrow3c=0\\ \Rightarrow c=0\)
Vậy \(P=\dfrac{a+b-2019c}{a+b+2018c}=\dfrac{a+b}{a+b}=1\)

\(A=\dfrac{x-1}{x^2-1}=\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\)
a) ĐKXĐ:
\(\left\{{}\begin{matrix}x-1\ne0\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
b) \(A=\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\)
c) Thay \(x=-2\) vào A, ta có:
\(A=\dfrac{1}{-2+1}=-1\)
Vậy khi x = -2 thì A = -1
a) ĐKXĐ: \(x\ne\pm1\)
b) \(\dfrac{x-1}{x^2-1}=\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\)
c) Khi x = - 2
\(\dfrac{1}{\left(-2\right)+1}=\dfrac{1}{-1}=-1\)
Vậy khi x = - 2 thì biểu thức có giá trị bằng - 1

a,Ta có: a^2 + b^2 + c^2 = ab + bc + ca
<=> 2.a^2 + 2.b^2 + 2.c^2 = 2.ab + 2.bc + 2.ca
<=> ( a^2 - 2ab + b^2 ) + ( b^2 - 2bc +c^2 ) + ( c^2 - 2ac + a^2 ) =0
<=> (a-b)^2 + (b-c)^2 + (c -a)^2 =0 (1)
Vì (a-b)^2≧0 ; (b-c)^2≧0 ; (c -a)^2 ≧ 0 với mọi a,b,c.
=> (a-b)^2 + (b-c)^2 + (c -a)^2 ≧ 0 (2)
Từ (1) và (2) :
=>a - b = 0; b - c = 0 ; c - a = 0 => a=b=c
Vậy a=b=c.
b,Ta có:(a+b+c)^2=3(a^2+b^2+c^2)
<=>a^2+b^2+c^2+2ab+2ac+2bc=3a^2+3b^2+3c^2
<=>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2=0
<=>-2a^2-2b^2-2c^2+2ab+2ac+2bc=0
<=>(-a^2+2ab-b^2)+(-b^2+2bc-c^2)+(-a^2+2ac-c^2)=0
<=>(-a+b)^2+(-b+c)^2+(-a+c)^2=0(1)
ta có:(-a+b)^2≧0, (-b+c)^2≧0, (-a+c)^2≧0(2)với mọi a,b,c.
từ (1)và (2)=>(-a+b)^2=0; (-b+c)^2=0; (-a+c)^2=0
<=>-a+b=0; -b+c=0; -a+c=0
<=>a=b=c
c, (a + b + c)^2=3(ab+ac+bc)
<=>a^2 +b^2+c^2+2ab+2ac+2bc -3ab-3ac-3bc=0
<=>a^2+b^2+c^2-ab-ac-bc=0
<=> 2a^2+2b^2+2c^2-2ab-2ac-2bc=0
<=> (a^2 - 2ab + b^2) + (b^2 - 2bc + c^2) + (c^2 - 2ca + a^2) = 0
<=> (a - b)^2 + (b - c)^2 + (c - a)^2 = 0
<=> a = b = c
Chúc bạn học tốt![]()
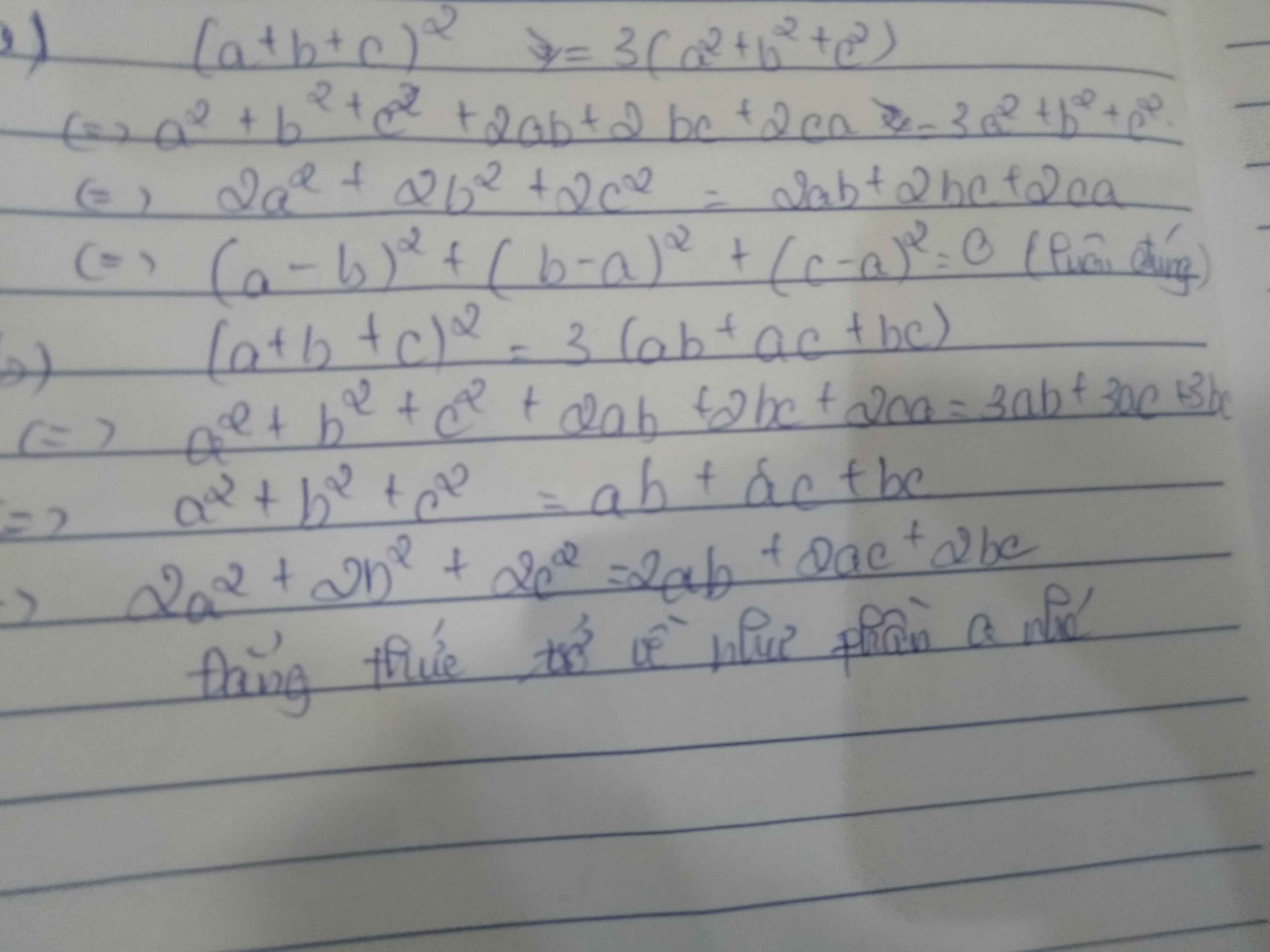
\(\frac{1}{\left(a+b+c\right)^2-3\left(ab+bc+ac\right)}\)
Điều kiện : \(\frac{1}{\left(a+b+c\right)\left(a+b+c\right)-3ab+3bc+3ac}\Rightarrow\hept{\begin{cases}a\ne0\\b\ne0\\c\ne0\end{cases}}\)