Cho số thực x và y thỏa mãn x+y-xy=155 và x2+y2=325.Tìm giá trị của |x3-y3|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3

Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
![]()
![]() (do
x
2
+
y
2
=
2
)
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
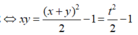
Từ ![]()
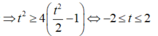
P = f(t) 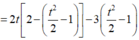
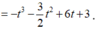
Xét f(t) trên [-2;2].
Ta có ![]()
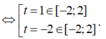
Bảng biến thiên
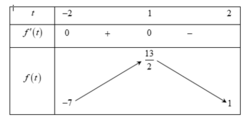
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có ![]()
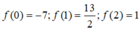
Suy ra kết luận.
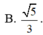
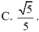
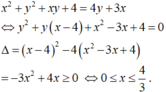
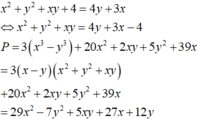
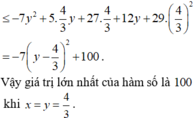
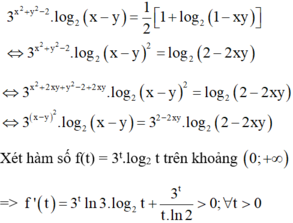

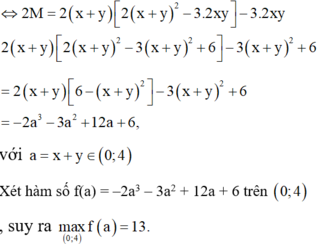

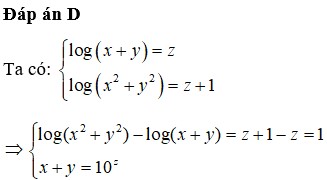
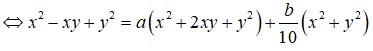
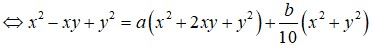
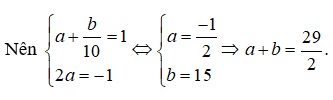
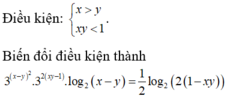
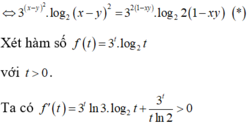

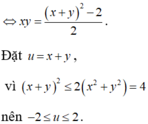
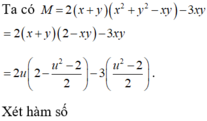
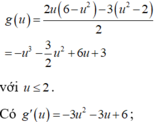
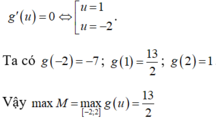
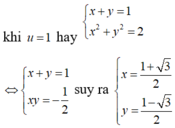
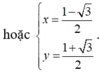
\(x^2+y^2=325\)
<=> \(\left(x+y\right)^2-2xy=325\)
Đặt: \(x+y=a;\)\(xy=b\)Khi đó ta có:
\(a-b=155\) (1)
và \(a^2-2b=325\)
Từ (1) ta có: \(b=a-155\) thay vào (2) ta được:
\(a^2-2\left(a-155\right)=325\)
giải ra tìm được: \(\orbr{\begin{cases}a=5\\a=-3\end{cases}}\) => \(\orbr{\begin{cases}a=5;b=-150\\a=-3;b=-158\end{cases}}\)
TH1: \(\hept{\begin{cases}a=5\\b=-150\end{cases}}\) ,=> \(\hept{\begin{cases}x+y=5\\xy=-150\end{cases}}\)
\(x^2+y^2=325\)
<=> \(\left(x-y\right)^2+2xy=325\)
<=> \(\left(x-y\right)^2=325-2xy=625\)
<=> \(\left|x-y\right|=25\)
=> \(\left|x^3-y^3\right|=\left|\left(x-y\right)\left(x^2+y^2+xy\right)\right|=\left|x-y\right|\left(x^2+y^2+xy\right)=4375\)
TH2: bn tự lm tiếp nhé