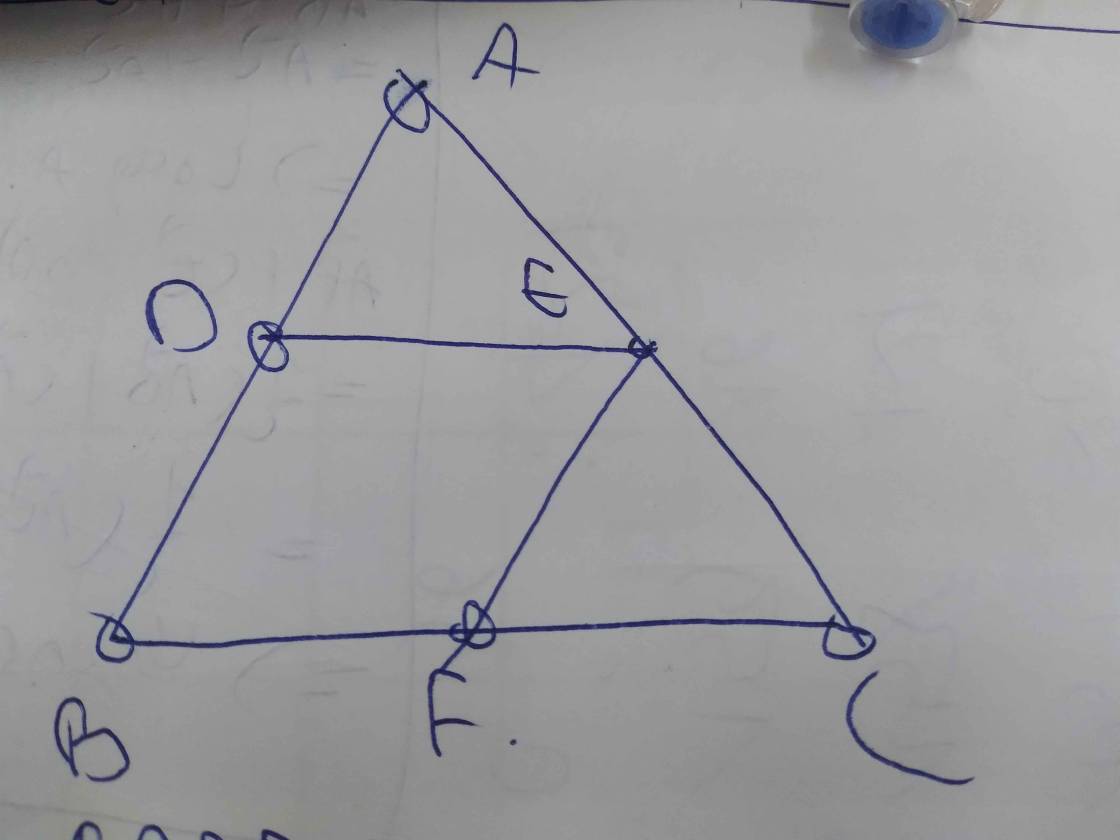
Cho tam giác ANC có AB=5cm, ÁC=9cm. Kẻ đường thẳng đ song song với BC cắt AB, ÁC thứ tự tại E, F. Xác định vị trí điểm E sao cho AE=CF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
13 tháng 1 2018
Lời giải:
Vì $EF$ song song với $BC$ nên áp dụng định lý Thales ta có:
\(\frac{AE}{AB}=\frac{AF}{AC}\Leftrightarrow \frac{AE}{5}=\frac{AF}{9}\)
\(\Leftrightarrow 9AE=5AF\)
Mà \(AF=AC-FC=9-FC\)
\(\Rightarrow 9AE=5(9-FC)\)
Khi \(AE=CF\Rightarrow 9AE=5(9-AE)\)
\(\Leftrightarrow 14AE=45\Leftrightarrow AE=\frac{45}{14}\) (cm) \((<5\) cm)
Vậy điểm E nằm trên đoạn thẳng $AB$ sao cho \(AE=\frac{45}{14}\) cm
NX
5 tháng 9 2023
Ta đặt: \(S_{BEMF}=S_1;S_{ABC}=S\)
Kẻ \(AK\perp BC\) ; \(AK\) cắt \(EM\left\{H\right\}\)
Ta có: \(S_1=EM.HK\)
\(\Leftrightarrow S=\dfrac{1}{2}BC.AK\)
\(\Leftrightarrow\dfrac{S_1}{S}=2\dfrac{EM}{BC}.\dfrac{KH}{AK}\)
Đặt \(MA=x;MC=y\) . Theo định lý Thales ta có:
\(\dfrac{EM}{BC}=\dfrac{x}{x+y};\dfrac{HK}{AK}=\dfrac{x}{x+y}\)
\(\Leftrightarrow\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\)
Áp dụng bất đẳng thức Cosi dạng \(\dfrac{ab}{\left(a+b\right)^2}\le\dfrac{1}{4}\) ta được:
\(\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\le\dfrac{1}{2}\) hay \(S_1\le\dfrac{1}{2}S\)
\(\Leftrightarrow MaxS_1=\dfrac{1}{2}S\)
\(\Leftrightarrow\) \(M\) là trung điểm của \(AC\)
5 tháng 3 2023
ND//AB
=>CN/CA=CD/CB
=>CN=CD
=>ΔNCD đều
=>NC=ND=CD
DM//AC
=>BD/BC=BM/BA
=>BD=BM
góc B=60 độ
=>ΔBMD đều
=>BM=BD=MD
góc MDC=180-60=120 độ
góc BDN=180-60=120 độ
=>góc MDC=góc BDN
Xét ΔBDN và ΔMDC có
BD=MD
góc BDN=góc MDC
DN=DC
=>ΔBDN=ΔMDC
=>BN=MC
=>BI=IN=KM=KC
Xét ΔKCD và ΔIND có
KC=IN
góc KCD=góc IND
CD=ND
=>ΔKCD=ΔIND
=>KD=ID
ΔKCD=ΔIND
=>góc IDN=góc KDC
=>góc KDI=60 độ
=>ΔKID đều
