Cho tam giác ABC có (O;r) là đường tròn nội tiếp, (O) tiếp xúc CA và BC lần lượt tại M và N. Các tia AO, BO cắt đường thẳng MN lần lượt tại P,Q. Gọi E và F theo thứ tự là trung điểm của AB,AC.
a) CMR: Tứ giác ABPQ nội tiếp ? b) CMR: 3 điểm E,Q,F thẳng hàng ?
c) Tia EO cắt cạnh AC tại D, đường thẳng MN cắt đường cao AH của tam giác ABC tại E. CMR: ^BAC=90 <=> AD=AE ?
d) CMR: \(\frac{MP+NQ+PQ}{AB+BC+CA}=\frac{r}{OC}\) ?

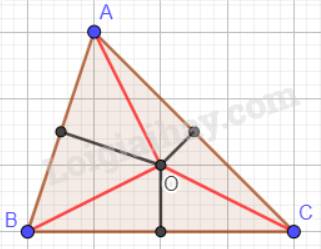
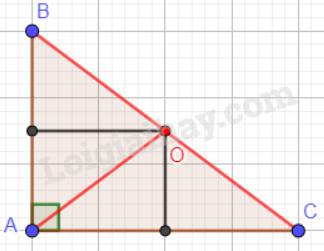
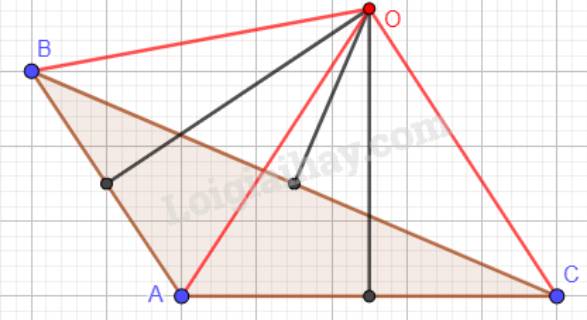
A B C M N O E F D H R Q P G
a) Dễ thấy: ^CMN = 900 - ^ACB/2; ^AOQ = ^OAB + ^OBA = 900 - ^ACB/2 => ^CMN = ^AOQ
=> Tứ giác AOQM nội tiếp => ^AQO = ^AMO = 900 (1)
Tương tự ta có: Tứ giác BOPN nội tiếp => ^BPO = ^BNO = 900 (2)
Từ (1) và (2) => ^AQO = ^BPO hay ^AQB = ^BPA => Tứ giác ABPQ nội tiếp (đpcm).
b) Xét \(\Delta\)AQB vuông tại Q: E là trung điểm cạnh AB => ^EQB = ^EBQ = ^ABC/2 = ^QBC
=> QE // BC (2 góc so le trong bằng nhau). Mà EF là đường trung bình tam giác ABC nên EF // AB
Do đó 3 điểm E,Q,F thẳng hàng (Tiên đề Ơ-clit) (đpcm).
c) Sửa điểm E thành điểm R cho đỡ trùng.
+) C/m : ^BAC = 900 => AR = AC ?
Chứng minh tương tự câu b ta có: PE //AC, gọi G là hình chiếu của O trên cạnh AB
Do ^BAC = 900 => AB vuông góc AC. Từ đó: AC // OG // PE. Áp dụng hệ quả ĐL Thales thì có:
\(\frac{r}{AD}=\frac{OG}{AD}=\frac{EG}{EA}=\frac{PO}{PA}=\frac{ON}{AR}=\frac{r}{AR}\)=> AD=AR (đpcm).
+) C/m : AR = AD => ^BAC = 900 ?
Lại theo hệ quả ĐL Thales, ta có các tỉ số: \(\frac{OG}{AD}=\frac{r}{AR}=\frac{ON}{AR}=\frac{PO}{PA}=\frac{EO}{ED}\)
=> OG // AC (ĐL Thales đảo). Mà OG vuông góc AB => AB vuông góc AC hay ^BAC = 900 (đpcm).
d) Hệ thức cần chứng minh \(\Leftrightarrow r\left(AB+BC+CA\right)=OC\left(MN+2PQ\right)\)
\(\Leftrightarrow S_{ABC}=S_{CMON}+2S_{CPOQ}\Leftrightarrow2S_{AOB}=2S_{CPOQ}\Leftrightarrow S_{AOB}=S_{CPOQ}\)
\(\Leftrightarrow OG.AB=OC.PQ\Leftrightarrow\frac{PQ}{AB}=\frac{OG}{OC}\Leftrightarrow\frac{OQ}{OA}=\frac{OM}{OC}\)(Do tứ giác ABPQ nội tiếp)
\(\Leftrightarrow\Delta AOQ~\Delta COM\left(g.g\right)\Leftrightarrow\hept{\begin{cases}\widehat{AQO}=\widehat{CMO}\left(=90^0\right)\\\widehat{OAQ}=\widehat{OCM}\left(=\widehat{OMQ}\right)\end{cases}}\)(Điều này hiển nhiên đúng)
Vậy hệ thức cần chứng minh là đúng => ĐPCM.