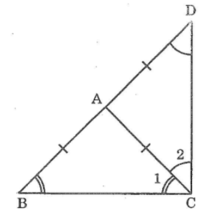
Tam giác ABC cân tại A. Lấy D sao cho A trung điểm của BD.Tính \(\widehat{BCD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
JP
1
28 tháng 7 2023
a: Xét ΔBMC và ΔDMA có
MB=MD
góc BMC=góc DMA
MC=MA
=>ΔBMC=ΔDMA
=>góc MBC=góc MDA
=>BC//AD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hbh
=>AB=CD=CA và AD=BC
b,c: Đề sai rồi bạn
B
1 tháng 3 2018
b) vì tam giác ABC là tam giác đều
\(\Rightarrow\)góc DBC=60 độ.
xét tam giác BDC và tam giác ADC có:
BD=AD(GT)
[góc DBC = góc DAC=60 độ (vì tam giác ABC đều)] hoặc [DC là cạnh chung]
BC=AC(GT)
\(\Rightarrow\)tam giác BDC=tam giác ADC(c.g.c hoặc c.c.c)
\(\Rightarrow\)góc BDC=góc ADC=90 độ( vì góc BDC+ góc ADC=180 độ).
áp dụng định lí tổng 3 góc bằng 180 độ vào tam giác BDC có
góc DBC+góc BDC+góc DCB= 180 độ
\(\Rightarrow\)góc DCB= 180 độ - 60 độ - 90 độ= 30 độ.
CM
18 tháng 6 2018
Ta có: ∆ABC cân tại A
⇒ AB = AC và ∠B = ∠C1 (tính chất tam giác cân) (1)
Lại có: AD = AB ( do A là trung điểm BD).
Suy ra: AD = AC do đó ∆ACD cân tại A
Nên ∠D =∠C2(tính chất tam giác cân) (2)
Mà ∠BCD =∠C1+ ∠C2 (3)
Từ (1); (2) và (3) suy ra: ∠BCD =∠B +∠D (4)
Trong ∆BCD, ta có:
∠BCD +∠B +∠D =180o (tổng 3 góc trong tam giác) (5)
từ (4) và (5) suy ra : 2 ∠BCD =180° hay∠BCD =90°
16 tháng 12 2021
Xét ΔBCD có
CA là đường trung tuyến
CA=BD/2
Do đó: ΔBCD vuông tại C
Tam giác ABC cân tại A \(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{ABC}=\widehat{ABC}\left(1\right)\end{cases}}\)
A là trung điểm của BD => AB = AD mà AB = AC => AD = AC
=> Tam giác CAD cân tại A \(\Rightarrow\widehat{ADC}=\widehat{ACD}\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{ACD}=\widehat{BCD}\)
Tam giác BDC có : \(\widehat{ABC}+\widehat{ADC}+\widehat{BDC}=180^o\)( Tổng 3 góc trong tam giác ) \(\Rightarrow\widehat{BCD}=\frac{180^o}{2}=90^o\)