làm câu c thôi aj
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




c)tính diện tích tam giác AOC
Hình vẽ đâu?Hay vd như góc A=___°,góc C=___° hay khác ?tự nhiên hỏi tính diện tích AOC ko có hình hoặc số đo góc làm sao tính đc.

c: Ta có: AM//BC
AE⊥BC
Do đó:AM⊥AE
Suy ra: \(\widehat{AME}+\widehat{AEM}=90^0\)
hay \(\widehat{AME}+\widehat{BAD}=90^0\)

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)

a:Thay x=49 vào A, ta được:
\(A=\dfrac{2\cdot7-10}{7-3}=\dfrac{4}{4}=1\)
b: \(B=\dfrac{3\sqrt{x}-15+20-2\sqrt{x}}{x-25}=\dfrac{1}{\sqrt{x}-5}\)

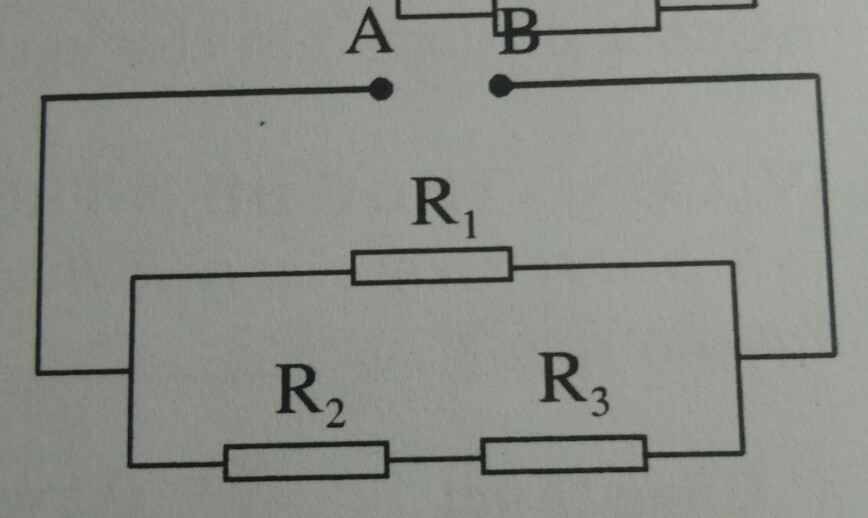
\(a.R_{tđ}=\dfrac{R_1.\left(R_2+R_3\right)}{R_1+R_2+R_3}=\dfrac{6.\left(2+4\right)}{6+2+4}=3\Omega\\ b.U_{AB}=I.R_{tđ}=2.3=6V\\ c.Vì.R_1//R_{23}\Rightarrow U_{AB}=U_1=U_{23}=6V\\ I_1=\dfrac{U_1}{R_1}=\dfrac{6}{6}=1A\\ I_{23}=I-I_1=2-1=1A\\ Vì.R_2ntR_3\Rightarrow I_{23}=I_2=I_3=1A\)

b: \(=\dfrac{x^2-x+1-3+1-x^2}{\left(x+1\right)\cdot\left(x^2-x+1\right)}=\dfrac{-x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{-1}{x^2-x+1}\)









 làm hộ câu b,c,d thôi ạ
làm hộ câu b,c,d thôi ạ
\(a,ĐK:x\ge0;x\ne9\\ P=\dfrac{\left(3\sqrt{x}+2\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}-3\right)\left(\sqrt{x}+1\right)-9\sqrt{x}+15}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\\ P=\dfrac{3x-7\sqrt{x}-6+2x-\sqrt{x}-3-9\sqrt{x}+15}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\\ P=\dfrac{5x-17\sqrt{x}+6}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(5\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{5\sqrt{x}-2}{\sqrt{x}+1}\)
\(b,x=4+2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\\ \Leftrightarrow P=\dfrac{5\sqrt{3}+5-2}{\sqrt{3}+1+1}=\dfrac{5\sqrt{3}+3}{2+\sqrt{3}}=\dfrac{\left(5\sqrt{3}+3\right)\left(2-\sqrt{3}\right)}{4-3}\\ P=7\sqrt{3}-9\)
\(c,\sqrt{x}\ge0\Leftrightarrow P=\dfrac{5\sqrt{x}-2}{\sqrt{x}+1}\ge\dfrac{5\cdot0-2}{0+1}=-2\\ P_{min}=-2\Leftrightarrow x=0\)