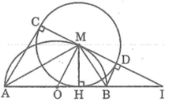
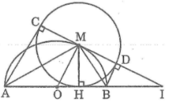
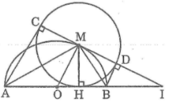
Cho nửa đường tròn (O) đường kính AB. Gọi M là điểm bất kỳ thuộc nửa đưởng tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tòn (M) ( C,D là tiếp điểm khác H )
a,CM: 3 điểm C,M,D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
b, CM: khi M di chuyển trên đường tròn (O) thì tổng AC + BD ko đổi
c,Giả sử CD cắt AB ở I. CM: OH.OI ko đổi



a: Xét (M) có
AC,AH là các tiếp tuyến
nên AC=AH và MA là phân giác của góc CMH(1)
Xét (M) co
BH,BD là các tiếp tuyến
nên BH=BD và MB là phân giác của góc DMH(2)
Từ (1), (2) suy ra góc CMD=2*90=180 độ
=>C,M,D thẳng hàng
b: AC+BD=AH+BH=AB=2R ko đổi