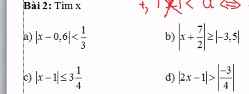giải hộ mik vs ạ
giải hộ mik vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
=>ΔBFC cân tại B
c: Xét ΔBFC có BA/BF=BE/BC
nên AE//CF
d: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc FC

\(A=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\left(dk:x\ge0,x\ne4\right)\\ =\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\\ =\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}\\ =\dfrac{x+2\sqrt{x}}{x-4}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Để \(A>1\) thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}>1\Leftrightarrow\dfrac{\sqrt{x}-\sqrt{x}+2}{\sqrt{x}-2}>0\Leftrightarrow2>0\left(LD\right)\)
\(\Leftrightarrow\sqrt{x}-2>0\Leftrightarrow x>4\left(tm\right)\)
Vậy \(x>4\) thì \(A>1\).

Bài 7:
\(\widehat{C}=180^0-70^0-40^0=70^0=\widehat{B}\)

\(\left\{{}\begin{matrix}2y-3x=7\\y+4x=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y-12x=28\\3y+12x=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}11y=55\\y+4x=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=5\\5+4x=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=1\end{matrix}\right.\)
Vậy nghiệm hpt: \(\left(x;y\right)=\left(1;5\right)\)

15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt

a: Ta có: \(\left|x-0.6\right|< \dfrac{1}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-0.6\ge0\\x-0.6< \dfrac{1}{3}\end{matrix}\right.\Leftrightarrow0.6\le x< \dfrac{14}{15}\)



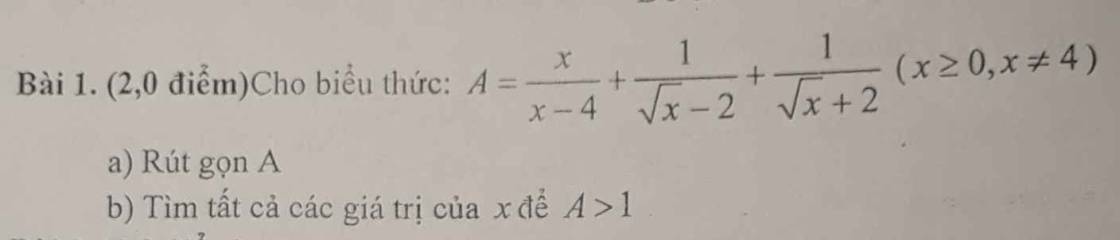
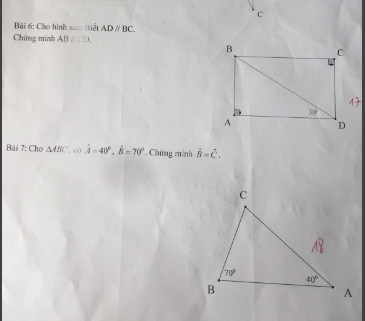 mik cần gấp. GIẢI CỤ THỂ HỘ MIK VS Ạ
mik cần gấp. GIẢI CỤ THỂ HỘ MIK VS Ạ