Tính A = \(\frac{x-y}{x+y}\) biết x2 - 2y2 = xy và y khác 0 , x + y khác 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tham khảo bài này nha
Link:https://olm.vn/hoi-dap/detail/266831819020.html
Chúc bạn học tốt

\(x^2-2y^2=xy\Rightarrow x^2-2y^2-xy=0\Rightarrow x^2-y^2-y^2-xy=0\)
\(\Rightarrow\left(x+y\right)\left(x-y\right)-y\left(x+y\right)=0\)
\(\Rightarrow\left(x+y\right)\left(x-2y\right)=0\Rightarrow x-2y=0\)\(\left(x+y\ne0\right)\)
\(\Rightarrow x=2y\)
Thay vào A tính đc giá trị của A

Ta có \(x^2-2y^2=xy\Leftrightarrow x^2-xy-2y^2=0\Leftrightarrow\left(x-2y\right)\left(x+y\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=2y\\x=-y\end{cases}}\)
với x=2y, thao vào, ta có A=1/3
với x=-y thay vào không thỏa mãn
^.^
\(x^2-2y^2=xy\Leftrightarrow x^2-xy-2y^2=0\)
\(\Leftrightarrow x^2+xy-2xy-2y^2=0\)
\(\Leftrightarrow x\left(x+y\right)-2y\left(x+y\right)=0\)
\(\Leftrightarrow\left(x-2y\right)\left(x+y\right)=0\)
\(\Rightarrow x-2y=0\) vì \(x+y\ne0\)
\(\Leftrightarrow x=2y\Rightarrow A=\frac{2y-y}{2y+y}=\frac{1}{3}\)

Ta có: \(x-y-xy=0\)
\(\Leftrightarrow x-y.\left(1+x\right)=0\)
\(\Leftrightarrow\left(1+x\right)-y.\left(1+x\right)=0+1\)
\(\Leftrightarrow\left(1+x\right).\left(1-y\right)=1\)
Bạn tìm x,y rùi tính \(\frac{1}{x}-\frac{1}{y}\)nhé

\(a)\) \(\frac{x^2y-xy}{x-1}=xy\)
\(\Leftrightarrow\)\(\frac{xy\left(x-1\right)}{x-1}=xy\)
\(\Leftrightarrow\)\(xy=xy\) ( đpcm )
\(b)\) \(\frac{x^2-y^2}{x^2+xy^2}=\frac{x-y}{x}\)
\(\Leftrightarrow\)\(\frac{\left(x+y\right)\left(x-y\right)}{x^2+xy^2}=\frac{x-y}{x}\)
\(\Leftrightarrow\)\(\frac{x+y}{x^2+xy^2}=\frac{1}{x}\)
\(\Leftrightarrow\)\(x\left(x+y\right)=x^2+xy^2\)
\(\Leftrightarrow\)\(x^2+xy=x^2+xy^2\)
\(\Leftrightarrow\)\(xy=xy^2\)
\(\Leftrightarrow\)\(y=y^2\) ( đề sai hay mình sai =.= )
Chúc bạn học tốt ~
a, \(\frac{x^2y-xy}{x-1}=\frac{xy\left(x-1\right)}{x-1}=xy\)
b,Sửa đề \(\frac{x^2-y^2}{x^2+xy}=\frac{x-y}{x}\)
\(\frac{x^2-y^2}{x^2+xy}=\frac{x^2-xy+xy-y^2}{x\left(x+y\right)}=\frac{x\left(x-y\right)+y\left(x-y\right)}{x\left(x+y\right)}=\frac{\left(x+y\right)\left(x-y\right)}{x\left(x+y\right)}=\frac{x-y}{x}\)

\(P=\dfrac{x^3+y^3}{x^3y^3}=\dfrac{\left(x+y\right)\left(x^2+y^2-xy\right)}{x^3y^3}=\dfrac{x^2y^2\left(x+y\right)}{x^3y^3}=\dfrac{x+y}{xy}=\dfrac{\left(x+y\right)^2}{xy\left(x+y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{x^2+y^2-xy}=\dfrac{4\left(x^2+y^2-xy\right)-3\left(x^2+y^2-2xy\right)}{x^2+y^2-xy}\)
\(=4-\dfrac{3\left(x-y\right)^2}{x^2+y^2-xy}\le4\)
\(P_{max}=4\) khi \(x=y=\dfrac{1}{2}\)

\(x^2-2y^2=xy\)
\(\Leftrightarrow\left(x^2+xy\right)-\left(2y^2-2xy\right)=0\)
\(\Leftrightarrow\left(x+y\right)\left(x-2y\right)=0\)
\(\Rightarrow x=2y\)
\(\Rightarrow A=\frac{x-y}{x+y}=\frac{2y-y}{2y+y}=\frac{y}{3y}=\frac{1}{3}\)
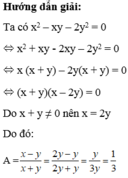
x2-2y2=xy
<=> (x-y)(x+y)=y(x+y)
Because y different from 0
=> y=x-y
<=> x=2y
=> Replace x by 2y
We have : the value of the A is 1/3
:v Mình đùa chút ^^ Đừng giận nha
mình đã làm được rồi , mọi người không cần đăng trả lợi nữa đâu ạ , xin cảm ơn !!!