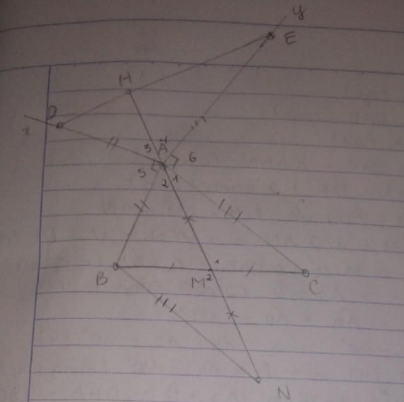
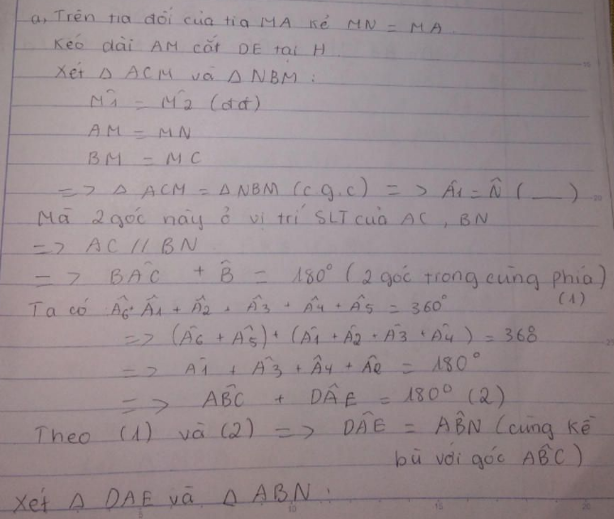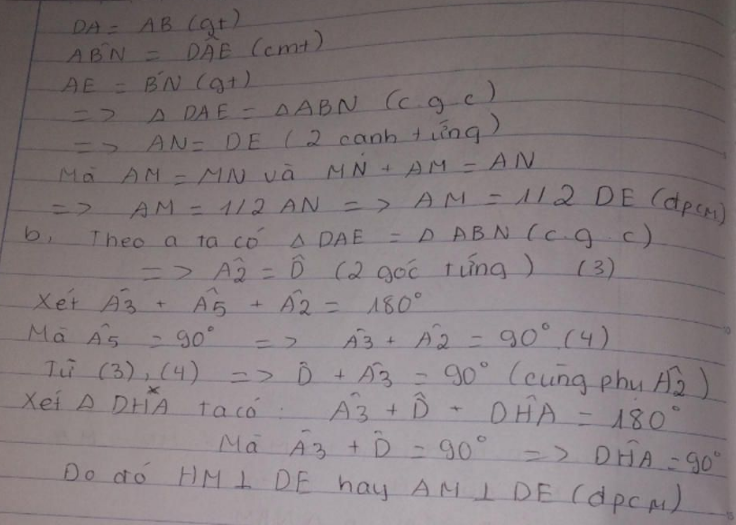Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD = AB. Trên nửa mặt phẳng không chứa B có bờ là AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE = AC. Chứng minh rằng: a) AM=\frac{DE}{2} b) AM \perp \ DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
1 tháng 9 2021
a) Trên tia đối tia MA lấy điểm F sao cho AM = AF (*)
Xét tam giác BFM và tam giác ACM có:
AM = FM (theo *)
Góc BMF = góc AMC (2 góc đối đỉnh)
BM = CM (vì M là trung điểm của BC)
=> Tam giác BFM = tam giác CAM (c.g.c)
=> AC = BF (2 cạnh tương ứng)
Vì AC = AE (gt) nên AE = BF
Ta có: góc F = góc CAM (vì tam giác BFM = tam giác CAM)
Mà 2 góc này ở vị trí so le trong
=> BF // AC (dấu hiệu nhận biết)
=> Góc BAC + góc ABF = 180 độ (2 góc trong cùng phía)
Mà góc BAC + góc DAE = 180 độ
=> Góc DAE = góc ABF
Xét tam giác ABF và tam giác ADE có:
AB = AD (gt)
Góc DAE = góc ABF (chứng minh trên)
AE = BF (2 cạnh tương ứng)
=> Tam giác ADE = tam giác BAF (c.g.c)
=> AF = DE (2 cạnh tương ứng)
Lại có: AM = AF : 2 => AM = DE : 2 (đpcm)
b) Gọi giao điểm của AM và DE là N
Ta có: tam giác ADE = tam giác BAF (chứng minh trên)
=> Góc D = góc BAF (2 góc tương ứng)
Mà góc BAF + góc DAN = 180 độ - góc BAD = 180 độ - 90 độ = 90 độ
=> Góc D + góc DAN = 90 độ
=> Tam giác ADN vuông tại N
hay AM _|_ DE (đpcm)
1 tháng 1 2020
a, Để chứng tỏ DE = 2AM,ta tạo ra đoạn thẳng gấp đôi AM bằng cách lấy K trên tia đối của tia MA sao cho MK = MA,ta sẽ chứng minh AK = DE
Dễ thấy AC = BK, AC // BK . Xét \(\Delta ABK\)và \(\Delta DAE\), ta có :
AB = AD gt
BK = AE cùng bằng AC
\(\widehat{ABK}=\widehat{DAE}\)cùng bù với góc BAC
Do đó \(\Delta ABK=\Delta DAE(c.g.c)\)
\(\Rightarrow AK=DE\)hai cạnh tương ứng
Vậy AM = DE/2
b, Gọi H là giao điểm của MA và DE.Ta có \(\widehat{BAK}+\widehat{DAH}=90^0\)nên \(\widehat{D}+\widehat{DAH}=90^0\), do đó góc AHD = 900
30 tháng 12 2017
a) Kẻ MN là tia đối của tia MA và MN = MA
Kéo dài AM cắt DE tại H
Xét ΔΔAMC và ΔΔNMB có:
AM = NM (cho ở trên)
AMCˆAMC^ = NMBˆNMB^ (đối đỉnh)
MC = MB (suy từ gt)
=> ΔΔAMC = ΔΔNMB (c.g.c)
=> ACMˆACM^ = NBMˆNBM^ (2 góc t/ư)
mà 2 góc này ở vị trí so le trong nên AC // BN
=> BACˆBAC^ + ABNˆABN^ = 180o (trong cùng phía) (3)
Vì DA ⊥⊥ AB nên DABˆDAB^ = 90o;
EA ⊥⊥ AC nên EACˆEAC^ = 90o
Ta có: DAHˆDAH^ + DABˆDAB^ + BANˆBAN^ = 180o
=> DAHˆDAH^ + 90o + BANˆBAN^ = 180o
=> DAHˆDAH^ + BANˆBAN^ = 90o (1)
Lại có: EAHˆEAH^ + EACˆEAC^ + CANˆCAN^ = 180o
=> EAHˆEAH^ + 90o + CANˆCAN^ = 180o
=> EAHˆEAH^ + CANˆCAN^ = 90o (2)
Cộng vế (1) và (2) ta đc:
DAHˆDAH^ + BANˆBAN^ + EAHˆEAH^ + CANˆCAN^ = 90o + 90o
=> (DAHˆDAH^ + EAHˆEAH^) +(BANˆBAN^ + CANˆCAN^) = 180o
=> DAEˆDAE^ + BACˆBAC^ = 180o (4)
Từ (3) và (4) suy ra:
BACˆBAC^ + ABNˆABN^ = DAEˆDAE^ + BACˆBAC^
=> ABNˆABN^ = DAEˆDAE^
Do ΔΔAMC = ΔΔNMB (c/m trên)
=> AC = NB (2 cạnh t/ư)
mà AC = AE (gt)
=> NB = AE
Xét ΔΔABN và ΔΔDAE có:
AB = DA (gt)
ABNˆABN^ = DAEˆDAE^ (c/m trên)
NB = AE (c/m trên)
=> ΔΔABN = ΔΔDAE (c.g.c)
=> AN = DE 92 cạnh t/ư)
mà AM = 1212 AN nên AM = 1212 DE.