cho (O) và (O') ( bán kính (O) > bán kính (O') ) cắt nhau tại A,B. Vẽ hình bình hành OBO'C. CMR: ACOO' là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2022
Gọi K là giao của ABvà O'O
=>K là trug điểm của AB
Gọi H là giao của CB và O'O
=>H là trung điểm của CB
Xét ΔBAC có BK/BA=BH/BC
nên KH//AC
=>O'O//AC
Xét tứ giác ACOO' co
AC//OO'
AO=CO'
Do đó: ACOO' là hình thang cân
CM
8 tháng 10 2018
a) Viết chữ thích hợp vào chỗ chấm:
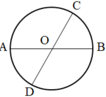
Đây là hình tròn tâm O.
- Các bán kính có trong hình tròn là: OA, OB, OC, OD.
- Các đường kính có trong hình tròn là: AB, DC.
b) Đúng ghi Đ, sai ghi S:
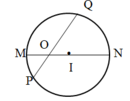
Đây là hình tròn tâm I
- Các bán kính có trong hình tròn là: IM, IN 
- Đường kính có trong hình tròn là: MN 
- Các bán kính có trong hình tròn là: OQ và OP
- Đường kính có trong hình tròn là PQ 
17 tháng 5 2022
a: Ta có: D nằm trên đường trung trực của AB
nên DA=DB
hay ΔDAB cân tại D
Ta có: E nằm trên đường trung trực của AC
nên EA=EC
hay ΔEAC cân tại E
b: Vì O nằm trên đường trung trực của AB
nên OA=OB(1)
Vì O nằm trên đường trung trực của AC
nên OA=OC(2)
Từ (1) và (2) suy ra OA=OB=OC
hay (O;OA) đi qua B và C
PT
1
27 tháng 9 2021
Ta có: \(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{ONM}=\widehat{OQP}\)
mà \(\widehat{OMN}=\widehat{ONM}\)
nên \(\widehat{OPQ}=\widehat{OQP}\)
Xét ΔOMN có \(\widehat{OMN}=\widehat{ONM}\)
nên ΔOMN cân tại O
Suy ra: OM=ON
Xét ΔOQP có \(\widehat{OPQ}=\widehat{OQP}\)
nên ΔOQP cân tại O
Suy ra: OQ=OP
Ta có: OM+OP=MP
ON+OQ=NQ
mà OM=ON
và OP=OQ
nên MP=NQ
Xét hình thang MNPQ có MP=NQ
nên MNPQ là hình thang cân
27 tháng 9 2021
Ta có: \(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{ONM}=\widehat{OQP}\)
mà \(\widehat{OMN}=\widehat{ONM}\)
nên \(\widehat{OPQ}=\widehat{OQP}\)
Xét ΔOMN có \(\widehat{OMN}=\widehat{ONM}\)
nên ΔOMN cân tại O
Xét ΔOQP có \(\widehat{OPQ}=\widehat{OQP}\)
nên ΔOQP cân tại O
Ta có: MP=MO+OP
NQ=NO+OQ
mà MO=NO
và OP=OQ
nên MP=NQ
Xét hình thang MNPQ có MP=NQ
nên MNPQ là hình thang cân