Cho hình thang ABCD có 2 đáy AB và CD,2 đường chéo cắt nhau tại O,biết diện tích tam giác AOB = 4 cm2,diện tích tam giác BOC = 9cm2.Tính diện tích hình thang ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


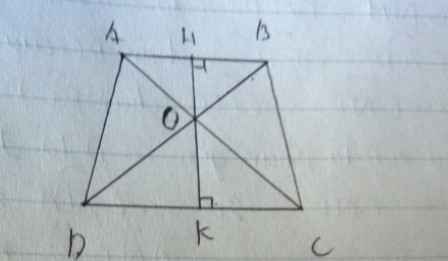
Kẻ AH vuông góc DC,BK vuông góc DC
Xéttứ giác ABKH có
AB//KH
AH//BK
=>ABKH là hình bình hành
=>AH=BK
=>\(S_{ADC}=S_{BDC}\)
=>\(S_{ADO}=S_{BOC}\)
\(\dfrac{S_{AOB}}{S_{BOC}}=\dfrac{OA}{OC}=\sqrt{\dfrac{4}{9}}=\dfrac{2}{3}\)
\(\dfrac{S_{AOD}}{S_{DOC}}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
=>\(\dfrac{4}{S_{AOD}}=\dfrac{S_{AOD}}{9}\)
=>\(S_{AOD}=6\left(cm^2\right)\)
=>\(S_{BOC}=6\left(cm^2\right)\)
\(S_{ABCD}=6+6+4+9=10+15=25\left(cm^2\right)\)

\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
 hình đây bn
hình đây bn
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
Trong hình thang ABCD cho ta: SAOD = SBOC = 9 cm2
Xét 2 tam giác AOB và AOD có chúng đường cao kẻ từ A nên 2 đáy OB và OD sẽ tỉ lệ với diện tích.
Suy ra OB/OD = 4/9
Mặt khác, 2 tam giác BOC và DOC có chúng đường cao kẻ từ C nên 2 diện tích sẽ tỉ lệ với 2 đáy.
Mà OB/OD = 4/9 nên SBOC/SDOC = 4/9
Diện tích tam giác DOC: 9 : 4 x 9 = 20,25 (cm2)
Diện tích hình thang ABCD: 4 + 9 + 9 + 20,25 = 42,25 (cm2)