Cho tam giác ABC cân tại A có \(\widehat{A}\)=\(30^o\),BC = 20 cm. Trên cạnh AC lấy điểm C sao cho \(_{\widehat{CDB}=60^o}\).Tính độ dài AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
21 tháng 2 2018
Tam giác ABC cân tại A, có góc A bằng 30 độ, suy ra góc B và C đều bằng 75 độ
vẽ hình ra nhé, kéo dài BD
từ A hạ đường vuông góc với BD cắt BD tại E
từ A cũng hạ đường vuông góc với BC cắt BC tại F
do góc BDC = 60 độ (đề bài cho)
nên góc ABE bằng 75-60=15 độ
xét 2 tam giác ABE và ABF
- AB chung
- góc BAF = góc ABE = 15 độ
- góc AFB = góc AEB = 90 độ
suy ra 2 tam giác bằng nhau (góc - cạnh - góc)
suy ra AE = BF = 1/2 BC = 1cm
xét tam giác nhỏ ADF ta có
- tam giác này vuông tại F
- góc DAF = 45 độ
suy ra tam giác này vuông cân tại F
suy ra AD = căn 2 AF = căn 2 cm
giải thích thêm chỗ góc DAF = 45 độ
do hai tam giác lớn cm bên trên bằng nhau suy ra góc BAF = góc ABE = 75 độ
góc BAC = 30 độ (đề bài cho)
suy ra góc DAF = 45 độ
P/s: chưa chắc đúng nha
Chúc các bn hok tốt !
31 tháng 7 2018
ΔABC cân tại A mà BACˆ=300
⇒ABCˆ=ACBˆ=1800−3002=750
Từ A, kẻ AE⊥BD (E∈BD)
kẻ AF⊥BC (F∈BC)
Vì CBDˆ=600(giả thiết)
⇒ABEˆ=750−600=150
Xét ΔABE và ΔBAF có:
AFBˆ=AEBˆ(=900)
Cạnh AB chung
BAFˆ=AEBˆ(=150)
⇒ΔABE=ΔBAF (g.c.g)
⇒AE=BF=12BC=1cm
Mặt khác, trong ΔBDC có:
DBCˆ=600
DCBˆ=750
⇒BDCˆ=450
⇒BDCˆ=ADEˆ (đối đỉnh)
Mà ΔADE vuông tại E
⇒ΔADE vuông cân tại E
⇒AE=ED
Mà AE=BF=1cm (cmt)
⇒ED=1cm
Áp dụng định lí Pytago, ta có:
AD2=EA2+ED2
⇒AD2=12+12=1+1=2
⇒AD=2–√
Vậy AD=2–√
9 tháng 2 2019
Đỗ Hoài Chinh mình không hiểu chỗ AF=BF=12BC=1cm
đáng lẽ 12BC phải bằng 24cm chứ?
giải thích hộ mình nhé
KN
16 tháng 8 2016
Tam giác ABC cân tại A, có góc A bằng 30 độ, suy ra góc B và C đều bằng 75 độ
vẽ hình ra nhé, kéo dài BD
từ A hạ đường vuông góc với BD cắt BD tại E
từ A cũng hạ đường vuông góc với BC cắt BC tại F
do góc BDC = 60 độ (đề bài cho)
nên góc ABE bằng 75-60=15 độ
xét 2 tam giác ABE và ABF
- AB chung
- góc BAF = góc ABE = 15 độ
- góc AFB = góc AEB = 90 độ
suy ra 2 tam giác bằng nhau (góc - cạnh - góc)
suy ra AE = BF = 1/2 BC = 1cm
xét tam giác nhỏ ADF ta có
- tam giác này vuông tại F
- góc DAF = 45 độ
suy ra tam giác này vuông cân tại F
suy ra AD = căn 2 AF = căn 2 cm
giải thích thêm chỗ góc DAF = 45 độ
do hai tam giác lớn cm bên trên bằng nhau suy ra góc BAF = góc ABE = 75 độ
góc BAC = 30 độ (đề bài cho)
suy ra góc DAF = 45 độ
31 tháng 12 2019
Vẽ \(\Delta BIC\) vuông can có đáy BC ( I và A cùng phia đối với BC ) . Ta có :
\(\widehat{CBI}=45^o,\widehat{IBD}=15^o,\widehat{DBA}=15^o\)
\(\Delta IAB=\Delta IAC\left(c.c.c\right)\)nên \(\widehat{IAB}=\widehat{IAC}=15^o\)
\(\Delta IAB=\Delta DBA\left(g.c.g\right)\)nên \(IB=AD\)
Xét \(\Delta BIC\)vuông cân , ta có :
\(BI^2+IC^2=BC^2=2^2=4\)
\(\Rightarrow2BI^2=4\)
\(\Rightarrow BI=\sqrt{2}\left(cm\right)\)
Do đó \(AD=\sqrt{2}\left(cm\right)\)
Chúc bạn học tốt !!!
18 tháng 9 2023
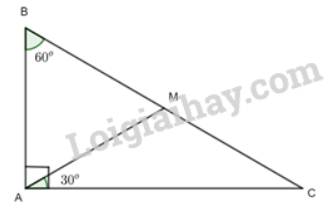
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.