Tính tổng: \(3\)\(\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(=\left(x^{16}-1\right)\left(x^{16}+1\right)\)
\(=x^{32}-1\)
Bạn tham khảo nhé!

b: Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=0\)
\(\Leftrightarrow\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24=0\)
\(\Leftrightarrow\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24=0\)
\(\Leftrightarrow x^2+7x+6=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-6\end{matrix}\right.\)

a)(x+1)(x+2)(x+3)(x+4)+1
=(x+1)(x+4)(x+2)(x+3)+1
=(x2+5x+4)(x2+5x+6)+1
Đặt a=(x2+5x+4) thì (x2+5x+4)(x2+5x+6)+1
= a.(a+2)+1
=a2+2a+1
=(a+1)2
Thay: =(x2+5x+4+1)2
=(x2+5x+5)2
b)(x+2)(x+4)(x+6)(x+8)+16
=(x+2)(x+8)(x+4)(x+6)+16
=(x2+10x+16)(x2+10x+24)+16
Đặt a=(x2+10x+16) thì (x2+10x+16)(x+5x+24)+1
= a.(a+8)+16
=a2+8x+16
=(a+4)2
Thay: =(x2+10x+16+4)2
=(x2+5x+20)2
a)(x+1)(x+2)(x+3)(x+4)+1
=[(x+1)(x+4][(x+2)(x+3)]+1
=(x2+5x+4)(x2+5x+6)+1
Đặt a=(x2+5x+4)
Ta có: (x2+5x+4)(x2+5x+6)+1
= a.(a+2)+1
=a2+2a+1
=(a+1)2
=(x2+5x+4+1)2
=(x2+5x+5)2
b)(x+2)(x+4)(x+6)(x+8)+16
=(x+2)(x+8)(x+4)(x+6)+16
=(x2+10x+16)(x2+10x+24)+16
Đặt a=(x2+10x+16)
Ta có:(x2+10x+16)(x+5x+24)+1
= a.(a+8)+16
=a2+8x+16
=(a+4)2
=(x2+10x+16+4)2
=(x2+5x+20)2
Mk yêu bé Shin-Conan lém![]()
![]()

quá dễ tách ra thành 1\x-1\x+1+1\x+1-1\x+2+1\x+2-1\x+3+1\x+3-1\x+4+...+1\x+5-1\x+6
=1\x-1\x+6
=6\x(x+6)
\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+2\right)\left(x+3\right)}+\frac{1}{\left(x+3\right)\left(x+4\right)}+\frac{1}{\left(x+4\right)\left(x+5\right)}+\frac{1}{\left(x+5\right)\left(x+6\right)}\)\(=\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}+\frac{1}{x+3}-\frac{1}{x+4}+\frac{1}{x+4}-\frac{1}{x+5}+\frac{1}{x+5}-\frac{1}{x+6}\)
\(=\frac{1}{x}-\frac{1}{x+6}\)\(=\frac{6}{x\left(x+6\right)}\)

1: \(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{8}\right)^6\)
\(\Leftrightarrow\left(\dfrac{1}{2}\right)^{4x}=\left(\dfrac{1}{2}\right)^{18}\)
=>4x=18
hay x=9/2
2: \(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{8}\right)^{36}\)
\(\Leftrightarrow\left(\dfrac{1}{2}\right)^{4x}=\left(\dfrac{1}{2}\right)^{108}\)
=>4x=108
hay x=27
3: \(\left(\dfrac{1}{81}\right)^x=\left(\dfrac{1}{27}\right)^4\)
\(\Leftrightarrow\left(\dfrac{1}{3}\right)^{4x}=\left(\dfrac{1}{3}\right)^{12}\)
=>4x=12
hay x=3

A= \(\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}+\frac{2}{x+3}-...+\frac{8}{x+5}-\frac{8}{x+6}\)
A=\(\frac{1}{x+1}+\frac{1}{x+3}+\frac{2}{x+4}+\frac{4}{x+5}-\frac{8}{x+6}\)
Rồi tiếp tục làm nhé bạn.
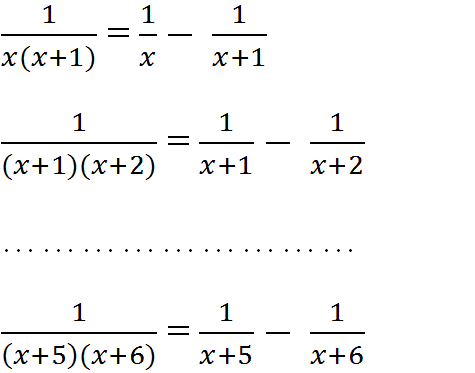
đấy là tích không phải tổng nhé
Đặt \(A=3\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(\Leftrightarrow\left(x^2-1\right)A=3\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(\Leftrightarrow\left(x^2-1\right)A=3\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(\Leftrightarrow\left(x^2-1\right)A=3\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(\Leftrightarrow\left(x^2-1\right)A=3\left(x^{16}-1\right)\left(x^{16}+1\right)\)
\(\Leftrightarrow\left(x^2-1\right)A=3\left(x^{32}-1\right)\)
\(\Leftrightarrow A=\frac{3\left(x^{32}-1\right)}{x^2-1}\)