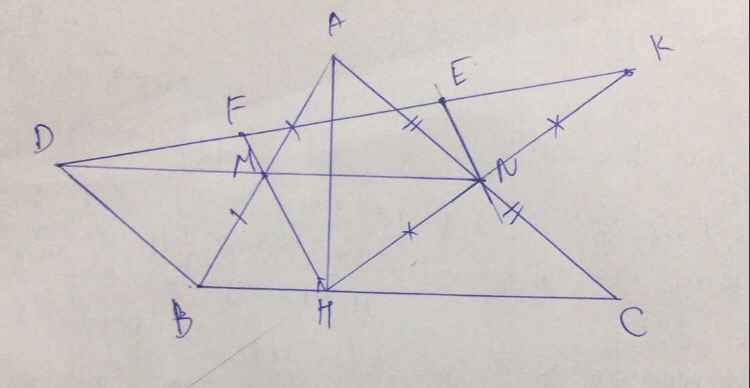
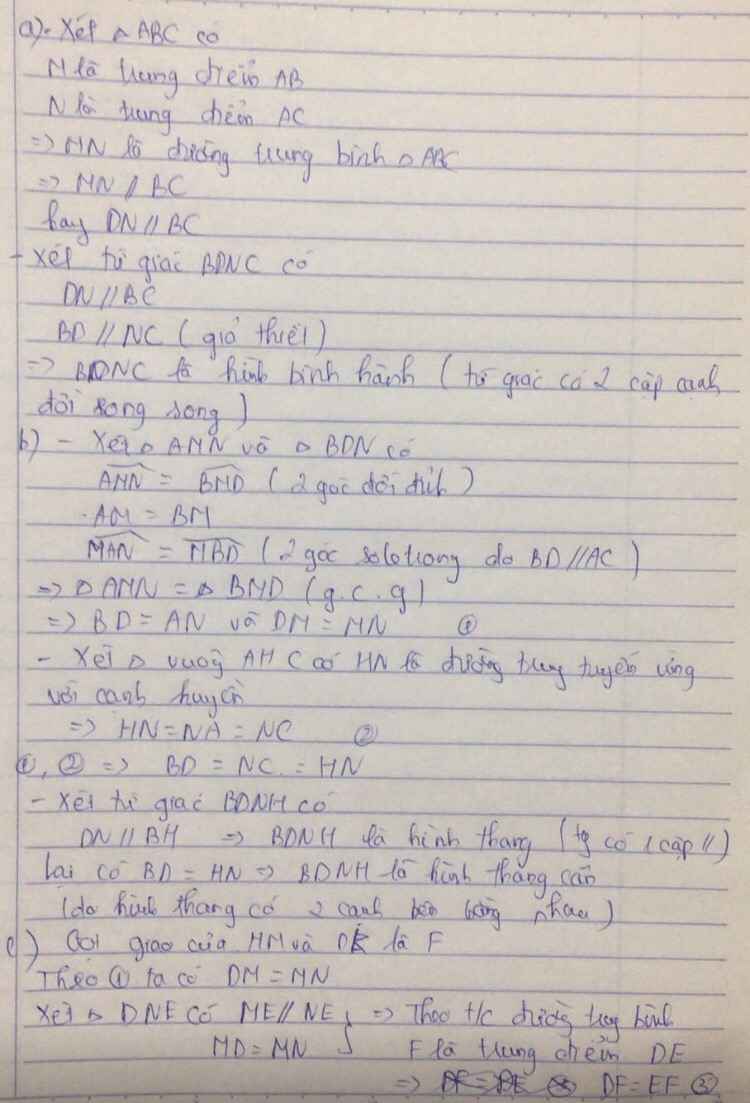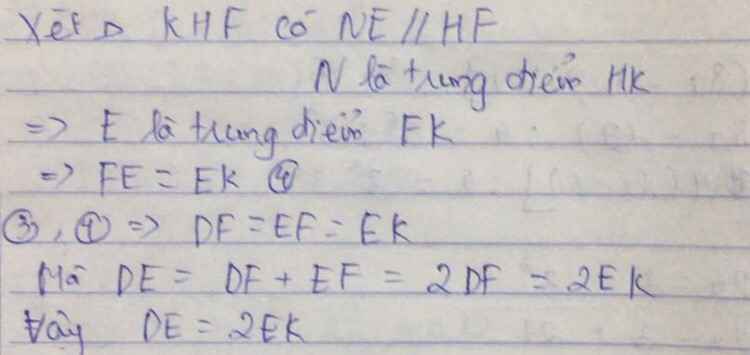Cho tam giác ABC vuông tại A, đường cao AH. Gọi I , K lần lượt là điểm đối xứng của H qua AB và AC. HI cắt AB ở D, HK cắt AC ở E.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Chứng minh: Tứ giác AIDE là hình bình hành và A là trung điểm của IK.
c) Gọi M là trung điểm của BC chứng minh: MI = MK.
các bạn giải và vẽ hình giúp mình luôn nha (thanks )