cho tứ giác ABCD có AB+BD<AC+CD Chứng minh AB<AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
và 
. 
và 
.
CM
30 tháng 7 2019
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: A
BV
0
23 tháng 5 2020
Bài làm
a) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\widehat{ABD}=\widehat{BDC}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong
=> AB // CD
b) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\frac{AB}{CD}=\frac{AD}{BC}=\frac{BD}{BD}\)
hay \(\frac{2}{8}=\frac{3}{BC}=\frac{BD}{BD}\)
=> BC = 8 . 3 : 2 = 12 ( cm )
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
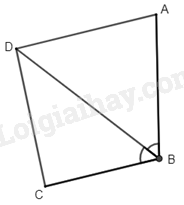
Xét \(\Delta ABD\) ta có: \(AD = AB\) (gt)
\( \Rightarrow \Delta ADB\) cân tại \(A\)
\( \Rightarrow \widehat {ADB} = \widehat {ABD}\)
Mà \(\widehat {ABD} = \widehat {CBD}\) (do \(BD\) là phân giác của góc \(B\))
\( \Rightarrow \widehat {ADB} = \widehat {CBD}\)
Mà hai góc ở vị trí so le trong
\( \Rightarrow AD\;{\rm{//}}\;BC\)
Suy ra \(ABCD\) là hình thang
17 tháng 11 2018
a) Ta có : \(AD=BC\left(gt\right)\)
=> ABCD là hình thang cân ( 2 cạnh bên = nhau )
b) Để MNPQ là hình chữ nhật thì \(\widehat{P}_1=90^o\)
Vì ABCD là hình thang cân ( câu a )
\(\Rightarrow AB//CD\)
Gọi I , K là 2 điểm nối từ A , B đến cạnh CD và vuông góc với CD
\(\Rightarrow AI//BK\) ( cùng vuông góc với CD )
Ta lại có : \(\widehat{P}_1=\widehat{K}\)( đ.vị ) (1)
Mà \(\widehat{K}=90^o\left(gt\right)\) (2)
Từ (1) và (2) \(\Rightarrow MNPQ\)là hình chữ nhật ( có góc = 90 độ )