Cho tam giác AOB vuông cân tại O, trên tia đối của tia OA lấy điểm C, trên tia đối của tia OB lấy điểm D sao cho OC=OD (OC\(\ne\)OA).
a) Chứng minh: ABCD là hình thang cân.
b) Trên nmp bờ là đường thẳng AC không chứa điểm B vẽ hình vuông ACMN. Các tứ giác ABDN, CBDM là hình gì? Vì sao?
c) Chứng minh:...
Đọc tiếp
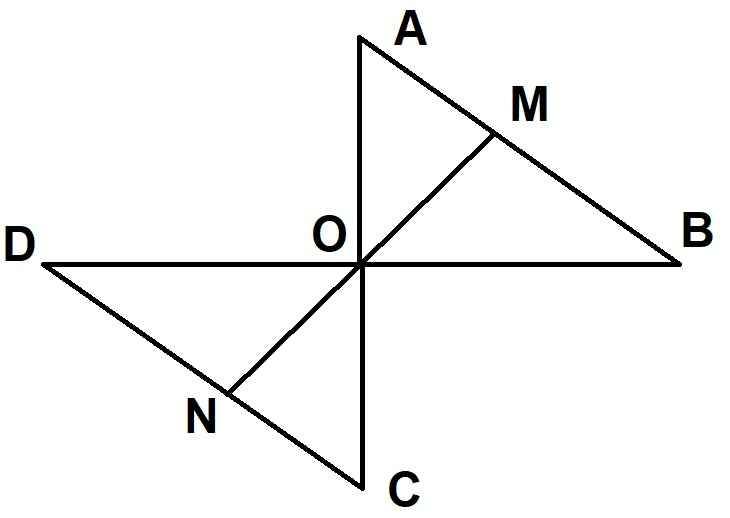
Cho tam giác AOB vuông cân tại O, trên tia đối của tia OA lấy điểm C, trên tia đối của tia OB lấy điểm D sao cho OC=OD (OC\(\ne\)OA).
a) Chứng minh: ABCD là hình thang cân.
b) Trên nmp bờ là đường thẳng AC không chứa điểm B vẽ hình vuông ACMN. Các tứ giác ABDN, CBDM là hình gì? Vì sao?
c) Chứng minh: \(\Delta\)ABC=\(\Delta\)NDA
a: Xét ΔOCD vuông tại O và ΔOAB vuông tại O có
OC/OA=OD/OB
nên ΔOCD đồng dạng với ΔOAB
=>góc OCD=góc OAB
=>CD//AB
=>ADCB là hình thang
mà AC=DB
nên ADCB là hình thang cân
b: Xét tứgiác ABDN có
AN//BD
AN=BD
Do đó: ABDN là hình bình hành
xét tứ giác CBDM có
CM//BD
CM=BD
Do đó: CBDM là hình bình hành