Mn giải giúp e câu c bài 2 đấy thôi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B2
0
TT
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
0
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
DT
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
2
10 tháng 12 2023
a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)
LT
giúp e giải gấp với ạ mấy câu lí thuyết thì ghi đáp án thôi còn mấy câu bài toán thì giải chi tiết ạ
0
XM
1
VL
2
Y
28 tháng 12 2021
Tham khảo:
Ve kêu đã tự khi nào
Mà ta cứ nghĩ mới vào đầu thu
Trường mới giờ đã thành xưa
Ngày nào mới đến giờ xa mất rồi
Bốn năm cứ nghĩ là dài
Cứ nghĩ học mãi học hoài chả xong
Bây giờ lại nhớ lại mong
Mái trường xưa cũ phượng hồng mùa thi.
LD
2
22 tháng 10 2021
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
22 tháng 10 2021
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
XV
1
TP
31 tháng 7 2021
43.a) \(m_{HCl\left(bđ\right)}=200.10,95\%=21,9\left(g\right)\)
=> \(n_{HCl\left(bđ\right)}=\dfrac{21,9}{36,5}=0,6\left(mol\right)\)
b) HCl phản ứng với NaOH là HCl dư
\(HCl+NaOH\rightarrow NaCl+H_2O\)
\(n_{HCl\left(dư\right)}=n_{NaOH}=0,05.2=0,1\left(mol\right)\)
=> \(n_{HCl\left(pứ\right)}=n_{HCl\left(bđ\right)}-n_{HCl\left(dư\right)}=0,6-0,1=0,5\left(mol\right)\)
c) \(CaCO_3+2HCl\rightarrow CaCl_2+H_2O+CO_2\)
\(n_{CaCO_3}=\dfrac{1}{2}n_{HCl\left(pứ\right)}=0,25\left(mol\right)\)
=> \(m_{CaCO_3}=0,25.100=25\left(g\right)\)
d) \(n_{CO_2}=\dfrac{1}{2}n_{HCl\left(pứ\right)}=0,25\left(mol\right)\)
=> \(V_{CO_2}=0,25.22,4=5,6\left(l\right)\)
e) \(m_{ddsaupu}=25+200-0,25.44=214\left(g\right)\)
Dung dịch A gồm CaCl2 và HCl dư
\(n_{CaCl_2}=\dfrac{1}{2}n_{HCl\left(pứ\right)}=0,25\left(mol\right)\)
\(C\%_{CaCl_2}=\dfrac{0,25.111}{214}.100=12,97\%\)
\(C\%_{HCl\left(dư\right)}=\dfrac{0,1.36,5}{214}.100=1,71\%\)
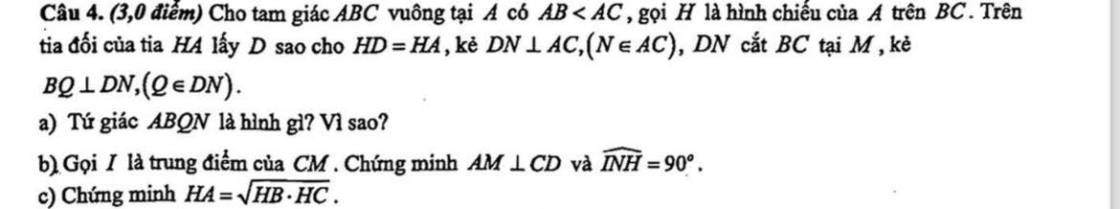
c: Ta có: \(\sqrt{x+4\sqrt{x-4}}=5\)
\(\Leftrightarrow\sqrt{x-4}+2=5\)
\(\Leftrightarrow\sqrt{x-4}=3\)
\(\Leftrightarrow x-4=9\)
hay x=13
c: Ta có: √x+4√x−4=5x+4x−4=5
⇔√x−4+2=5⇔x−4+2=5
⇔√x−4=3⇔x−4=3
⇔x−4=9⇔x−4=9
hay x=13