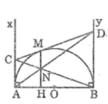
cho đường tròn ( O), đường kính AB, vẽ các tiếp tuyến Ax, By từ M trên đường tròn ( M khác A,B), vẽ tiếp tuyến thứ 3 cắt Ax ở C, cắt By ở D . gọi N là giao điểm của BC và AO.
a. cmr \(\dfrac{CN}{AC}=\dfrac{NB}{BD}\)
b) cmr \(MN\perp AB\)
c.CMR : \(\widehat{COD}=90^0\)

a) Ta có:AC⊥AB(gt) ;BD⊥AB(gt)
=> AC//BD
=> ∠CNA = ∠DNB(2 góc đối đỉnh)
∠ADB=∠NAC
=> △CAN đồng dạng ΔBND
=>\(\dfrac{CN}{BN}=\dfrac{AC}{BD}< =>\dfrac{CN}{AC}=\dfrac{NB}{BD}\) (đpcm)
c) AC;CD;BD là các tiếp tuyến của đg tròn(O)
Theo t/c của 2 tiếp tuyến cắt nhau ta đc:
Oc là tia p/g của góc AOC
OD là tia p/g của góc MOD
Mà góc AOC kề bù vs góc MOD
=>OC⊥OD=> góc COD=90o