Tìm giá trị nguyên của x để biểu thức có giá trị nguyên:
a, x3- 2a2+ 4/ x-2
b, x3-x2+2/ x-1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 1
Ta có 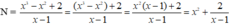
Để N nguyên 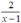 nguyên ⇒ x - 1 là ước của 2
nguyên ⇒ x - 1 là ước của 2
Ư ( 2 ) = 1 ; - 1 ; 2 ; - 2
x – 1 = 1 ⇒ x =2 (thỏa mãn điều kiện xác định);
x - 1 = -1 ⇒ x = 0 (thỏa mãn điều kiện xác định);
x - 1 = 2 ⇒ x = 3 (thỏa mãn điều kiện xác định);
x - 1 = -2 ⇒ x = -1 (thỏa mãn điều kiện xác định);
Vậy với x ∈ { -1;0;2;3 } thì phân thức N nhận giá trị nguyên

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

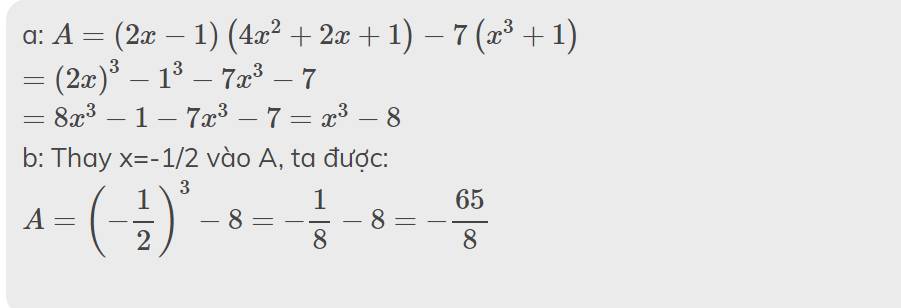
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3

Câu 1: x^3+y^3+3xy
=(x+y)^3-3xy(x+y)+3xy
=(x+y)^3-3xy+3xy
=1
Câu 2:
x^3-y^3-3xy
=(x-y)^3+3xy(x-y)-3xy
=1^3
=1
Câu 3:
\(x^2+y^2=\left(x+y\right)^2-2xy=4-2\cdot\left(-15\right)=4+30=34\)
Câu 4:
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=-8-3\cdot\left(-2\right)\cdot\left(-15\right)=-8-3\cdot30=-98\)
Câu 5: B
Câu 6: C
Câu 7: B
Câu 8: D
Câu 10: B
1) Nếu x+y=1, thì giá trị của biểu thức x3+y3+3xy là
A.2
B.3
C.4
D.cả A,B,C đều sai
2)Nếu x-y=1, thì giá trị của biểu thức x3-y3-3xy là
A.1
B.2
C.3
D.4
3) Cho x+y= -2, xy=-15 thì giá trị của biểu thức x2+y2 là.
A) 30 ; B) 32 ;C) 28 ; D) Cả A và B đều sai.
4) Với giả thiết bài 3, ta có giá trị của biểu thức x3+y3 là:
A) 80 ; B) 81; C) 82 ; D) Một kết quả khác
5) Với giả thiết bài 3, ta có giá trị của biểu thức x4+y4 là:
A. 706 ; B. 702 ; C. 708 ; D. 704
6)Giá trị nhỏ nhất của biểu thức P= x(x+1)(x+2)(x+3) là
A. 1 ; B. 2 ; C. -1 ; D.-2
7)Cho biểu thức M=2x2+9y2- 6xy-6x-12y+2037 . Giá trị nhỏ nhất của biểu thức M là
A. 2007 ; B. 2008 ; C; 2009 ; D. 2010
8) Với giả thiết bài 7 , biểu thức M đạt giá trị nhỏ nhất khi
A)x=5;y= 7/3
B)x= -5; y= 7/3
C) x=5; y= -7/3
D)cả A và C đều sai
9) Cho biểu thức Q= 2xy+6x-2y-2x2-y2+ 2015 .Giá trị lớn nhất của biểu thức Q là
A. 2010 ; B. 2012 ; C. 2020 ; D. Một kết quả khác

Ta có: \(B=x^3+3x^2+3x+9\)
\(=x^2\left(x+3\right)+3\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2+3\right)\)
Để B là số nguyên tố thì: \(\left[{}\begin{matrix}x+3=1\\x^2+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x^2=-2\left(voli\right)\end{matrix}\right.\)
Thay \(x=-2\) vào B ta được:
\(B=\left(-2+3\right)\left[\left(-2\right)^2+3\right]=7\) là số nguyên tố.
Vậy \(x=-2\)

a) ĐKXĐ: \(x\notin\left\{-3;2\right\}\)
b) Ta có: \(P=\dfrac{x^3+2x^2-5x-6}{x^2+x-6}\)
\(=\dfrac{x^3+3x^2-x^2-3x-2x-6}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2\left(x+3\right)-x\left(x+3\right)-2\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x+3\right)\left(x^2-x-2\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)}{x-2}=x+1\)
Với mọi x nguyên thỏa ĐKXĐ, ta luôn có: x+1 là số nguyên
hay P là số nguyên(đpcm)

\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Do \(x^2\left(x^2-x+5\right)\) chia hết \(x^2-x+5\)
\(\Rightarrow x^2-x+a\) chia hết \(x^2-x+5\)
\(\Rightarrow a=5\)
\(\frac{x^3-2x^2+4}{x-2}\inℤ\Leftrightarrow x^3-2x^2+4⋮x-2\)
\(\Leftrightarrow x^3-2x^2-\left(x^3-2x^2\right)+4⋮x-2\Leftrightarrow4⋮x-2\)
\(\Leftrightarrow x-2\in\left\{-1;2;-2;1;-4;4\right\}\Leftrightarrow x\in\left\{1;4;0;3;-2;6\right\}\)
b, \(\frac{x^3-x^2+2}{x-1}\inℤ\Leftrightarrow x^3-x^2+2⋮x-1\)
\(\Leftrightarrow x^3-x^2-\left(x^3-x^2\right)+2⋮x-1\)
\(\Leftrightarrow2⋮x-1\Leftrightarrow x-1\in\left\{-1;1;-2;2\right\}\)
\(\Leftrightarrow x\in\left\{0;2;-1;3\right\}\)