bài 1. Cho tam giác MPQ vuông tại M . MP < MQ . I là trung điểm của PQ . Từ I kẻ đường thẳng song song với MQ và MP lần lượt cắt MP tại K và cắt MQ tại H .a. Chứng minh tứ giác KHQP là hình thang.b. Chứng minh tứ giác MKIH là hình chữ nhật.c. Gọi O là trung điểm của MI . Chứng minh K đối xứng với H qua O.bài 2. Cho tam giác ABC vuông tại A , BC = 8 cm . Hai trung tuyến BM và CN cắt nhau tại G.a. Tính MN.b. Gọi K và I lần...
Đọc tiếp
bài 1. Cho tam giác MPQ vuông tại M . MP < MQ . I là trung điểm của PQ . Từ I kẻ đường thẳng song song với MQ và MP lần lượt cắt MP tại K và cắt MQ tại H .
a. Chứng minh tứ giác KHQP là hình thang.
b. Chứng minh tứ giác MKIH là hình chữ nhật.
c. Gọi O là trung điểm của MI . Chứng minh K đối xứng với H qua O.
bài 2.
Cho tam giác ABC vuông tại A , BC = 8 cm . Hai trung tuyến BM và CN cắt nhau tại G.
a. Tính MN.
b. Gọi K và I lần lượt là trung điểm của BG và CG.Chứng minh NMQK là hình bình hành.
c. Trên trung tuyến AI của tam giác ABC , lấy điểm H sao cho IA = IH . Chứng minh tứ giác ABHC là hình chữ nhật.
MONG MỌI NGƯỜI GIÚP MÌNH VỚI Ạ
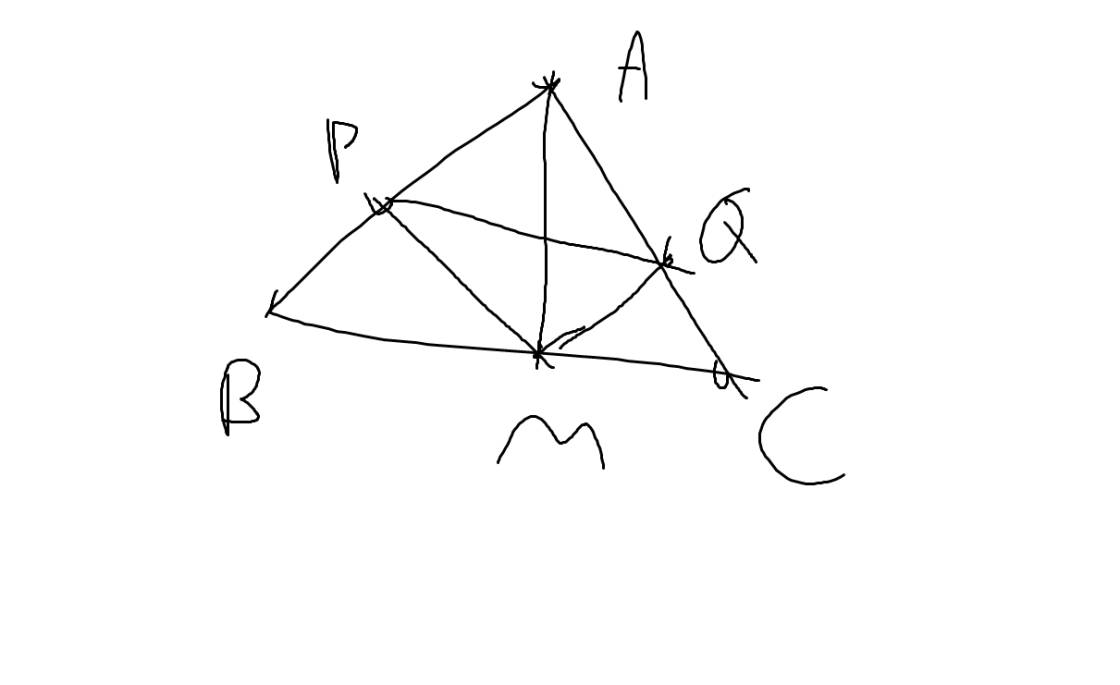
Bài 2:
b: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
K là trung điểm của GB
I là trung điểm của GC
Do đó: KI là đường trung bình của ΔGBC
Suy ra: KI//BC và \(KI=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra NM//KI và NM=KI
Xét tứ giác NMIK có
NM//KI
NM=KI
Do đó: NMIK là hình bình hành