2cos4x+4sin2xcos2x-\(\sqrt{2}\)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
\(\Leftrightarrow3\left(1-sin^22x\right)+4sin2x-4=0\)
\(\Leftrightarrow-3sin^22x+4sin2x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=\frac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{1}{2}arcsin\left(\frac{1}{3}\right)+k\pi\\x=\frac{\pi}{2}-\frac{1}{2}arcsin\left(\frac{1}{3}\right)+k\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\end{matrix}\right.\)
f/
\(\Leftrightarrow4\left(1-2sin^2\frac{x}{2}\right)-5sin\frac{x}{2}=1\)
\(\Leftrightarrow8sin^2\frac{x}{2}+5sin\frac{x}{2}-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\frac{x}{2}=-1\\sin\frac{x}{2}=\frac{3}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\pi+k4\pi\\x=2arcsin\left(\frac{3}{8}\right)+k4\pi\\x=2\pi-2arcsin\left(\frac{3}{8}\right)+k4\pi\end{matrix}\right.\)

e/
ĐKXĐ: ...
\(\Leftrightarrow\frac{2sin4x.cos2x}{cos2x}-2cos4x=2\sqrt{2}\)
\(\Leftrightarrow2sin4x-2cos4x=2\sqrt{2}\)
\(\Leftrightarrow sin4x-cos4x=\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(4x-\frac{\pi}{4}\right)=\sqrt{2}\)
\(\Leftrightarrow sin\left(4x-\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow4x-\frac{\pi}{4}=\frac{\pi}{2}+k2\pi\)
\(\Rightarrow x=\frac{3\pi}{16}+\frac{k\pi}{2}\)
d/
Đặt \(sin2x-cos2x=\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(\Rightarrow t^2-3t-4=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=4\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=-1\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\2x-\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{3\pi}{4}+k\pi\end{matrix}\right.\)

câu 1
⇒ \(\dfrac{cosx}{sinx}\) - \(\dfrac{sinx}{cosx}\) -\(\dfrac{2cos4x}{2sinxcosx}\) =0
⇔ \(\dfrac{cos^2x-sin^2x}{sinx.cosx}\) -\(\dfrac{cos4x}{sinx.cosx}\)= 0
⇔ \(\dfrac{cos2x-cos4x}{sinx.cosx}\) = 0
\(\left[{}\begin{matrix}cos2x=cos4x\\sin2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=4x+k2\pi\\2x=-4x+k2\pi\\2x=k\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-k\pi\\x=\dfrac{k\pi}{3}\\x=\dfrac{k\pi}{2}\end{matrix}\right.\) (k∈ Z)
câu 2 dùng công thức biến đổi tích thành tổng thành cos 4x + cos 2x sau đó phương trình trở thành sin x - cos 4x=0


Câu 2 bạn coi lại đề
3.
\(1+2sinx.cosx-2cosx+\sqrt{2}sinx+2cosx\left(1-cosx\right)=0\)
\(\Leftrightarrow sin2x-\left(2cos^2x-1\right)+\sqrt{2}sinx=0\)
\(\Leftrightarrow sin2x-cos2x=-\sqrt{2}sinx\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}sin\left(-x\right)\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=sin\left(-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=-x+k2\pi\\2x-\frac{\pi}{4}=\pi+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
4.
Bạn coi lại đề, xuất hiện 2 số hạng \(cos4x\) ở vế trái nên chắc là bạn ghi nhầm
5.
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=2cos^2\left(\frac{\pi}{4}-x\right)-1\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=cos\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=sin2x\)
\(\Leftrightarrow sin2x\left(sinx-cosx.sin2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\Leftrightarrow x=...\\sinx-cosx.sin2x-1=0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow sinx-1-2sinx.cos^2x=0\)
\(\Leftrightarrow sinx-1-2sinx\left(1-sin^2x\right)=0\)
\(\Leftrightarrow2sin^3x-sinx-1=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sin^2x+2sinx+1\right)=0\)
\(\Leftrightarrow...\)

Lời giải:
\(y=5+4\sin 2x\cos 2x=5+2\sin 4x\)
Ta thấy \(\sin 4x\in [-1;1], \forall x\in\mathbb{R}\Rightarrow 2\sin 4x\in [-2;2]\)
Để $y$ nhận giá trị nguyên thì $2\sin 4x$ phải nhận giá trị nguyên. Mà trong đoạn $[-2;2]$ có $5$ giá trị nguyên nên $y$ cũng có tất cả $5$ giá trị nguyên.
cho hỏi là trên 5+2sin4x nhưng sao chỉ tìm giá trị của 2sin4x vậy ạ ?

\(\Leftrightarrow2sin5x.sinx+1=2cos4x.sinx+2cos2x.sinx+3sinx\)
\(\Leftrightarrow2sin5x.sinx+1=sin5x-sin3x+sin3x-sinx+3sinx\)
\(\Leftrightarrow2sin5x.sinx-sin5x-2sinx+1=0\)
\(\Leftrightarrow sin5x\left(2sinx-1\right)-\left(2sinx-1\right)=0\)

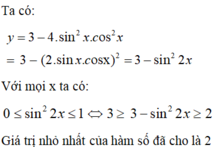
\(2\cos4x+4\sin2x\cos2x-\sqrt{2}=0\\ < =>2\cos4x+2\sin4x=\sqrt{2}\\ < =>2.\left(\cos4x+\sin4x\right)=\sqrt{2}\\ < =>2\sqrt{2}.\sin\left(4x+\dfrac{\pi}{4}\right)=\sqrt{2}\\ < =>\sin\left(4x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\\ < =>\left[{}\begin{matrix}4x+\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\4x+\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{-\pi}{48}+k\dfrac{\pi}{2}\\x=\dfrac{7\pi}{48}+k\dfrac{\pi}{2}\end{matrix}\right.\)
\(2\cos4x+4\sin2x.\cos2x-\sqrt{2}=0\\ < =>2.\cos4x+2.\sin4x=\sqrt{2}\\ < =>2\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}\\ < =>\sin\left(4x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\\ < =>\left[{}\dfrac{x+\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi}{x+\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi}}\\ < =>\left[{}\begin{matrix}x=\dfrac{-\pi}{12}+k2\pi\\x=\dfrac{7\pi}{12}+k2\pi\end{matrix}\right.\)