Tìm số tự nhiên n lớn nhất sao cho 29n là ước của 2015!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(29^n\varepsilon U\left(2003\right)\Leftrightarrow29^n\le2003\Rightarrow n< 3\)mà\(n\varepsilon N\Rightarrow n\varepsilon\left\{0;1;2\right\}\Rightarrow29^n\varepsilon\left\{1,29,841\right\}\left(1\right)\)
Lại có:\(2003⋮29^n\left(2\right)\)
Từ (1) và (2) => n = 0

a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
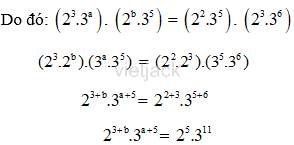
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y= 22.35.23.36=22.23.35.36=25.31122.35.23.36=22.23.35.36=25.311
Mà xy =23+b.3a+523+b.3a+5
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6

a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a=1.2.3.4.5.6.7.8.9.10.
=2^8.3^4.5^2.7
=(2^4.3^2.5)^2.7
Vậy n=2^4.3^2.5=720

1. Đặt \(ƯCLN\left(5n+3,6n+1\right)=d\) với \(d\ne1\)
\(\Rightarrow\left\{{}\begin{matrix}5n+3⋮d\\6n+1⋮d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}30n+18⋮d\\30n+5⋮d\end{matrix}\right.\)
\(\Rightarrow13⋮d\)
\(\Rightarrow d\in\left\{1,13\right\}\)
Nhưng vì \(d\ne1\) nên \(d=13\). Vậy \(ƯCLN\left(5n+3,6n+1\right)=13\)
2. Gọi \(ƯCLN\left(4n+3,5n+4\right)=d\)
\(\Rightarrow\left\{{}\begin{matrix}4n+3⋮d\\5n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}20n+15⋮d\\20n+16⋮d\end{matrix}\right.\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(ƯCLN\left(4n+3,5n+4\right)=1\) nên 2 số này nguyên tố cùng nhau. (đpcm)
3: Tương tự 2 nhưng khi đó \(d\in\left\{1,2\right\}\). Nhưng vì cả 2 số \(2n+1,6n+5\) đều là số lẻ nên chúng không thể có ƯC là 2. Vậy \(d=1\)
4. Tương tự 3.