Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, \(AC\) \(=\dfrac{a}{2}\), \(SC=BC=a\sqrt{2}\). Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A', B'. Tính thể tích V của khối chóp S.A'B'C.
A. \(V=\dfrac{a^3\sqrt{14}}{49}\)
B. \(V=\dfrac{a^3\sqrt{14}}{64}\)
C. \(V=\dfrac{a^3\sqrt{14}}{54}\)
D. \(V=\dfrac{4a^3}{61}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
23 tháng 7 2019
Chọn D.
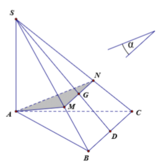
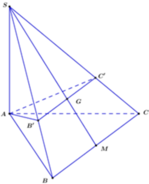
Do ( α ) đi qua G ∈ (SBC), song song với BC nên ( α ) cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
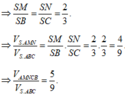
Do tam giác ABC vuông cân tại B, AC = a
2
nên ![]()
Do SA
⊥
(ABC) nên ![]()
![]()

CM
30 tháng 9 2018
Chọn B.
Dễ thấy AB ⊥ BC. Suy ra SB ⊥ BC, ∆ SMN đồng dạng với ∆ SCB, do đó

CM
25 tháng 9 2017
Chọn A.
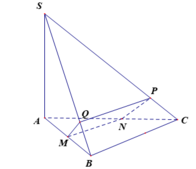
- Trong (SAB), từ M kẻ đường thẳng vuông góc với SB tại Q.
- Trong (SBC) từ Q kẻ đường thẳng vuông góc với SB cắt SC tại P.
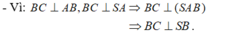
- Do đó BC// QP, trong (ABC) từ M kẻ đường thẳng song song với BC cắt AC tại N.
- Xét tứ giác MNPQ, ta có BC // QP nên tứ giác là là hình thang.
- Mặt khác:
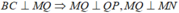
nên tứ giác MNPQ là hình thang vuông.

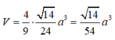

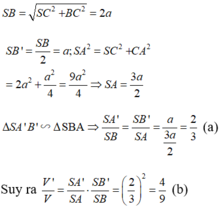
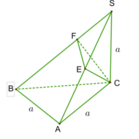

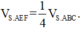
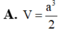
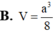
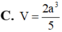
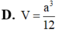
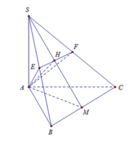


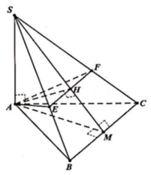

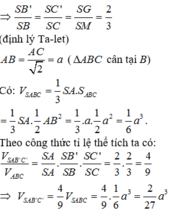
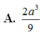
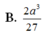
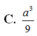
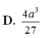


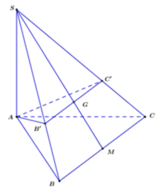
Chọn C