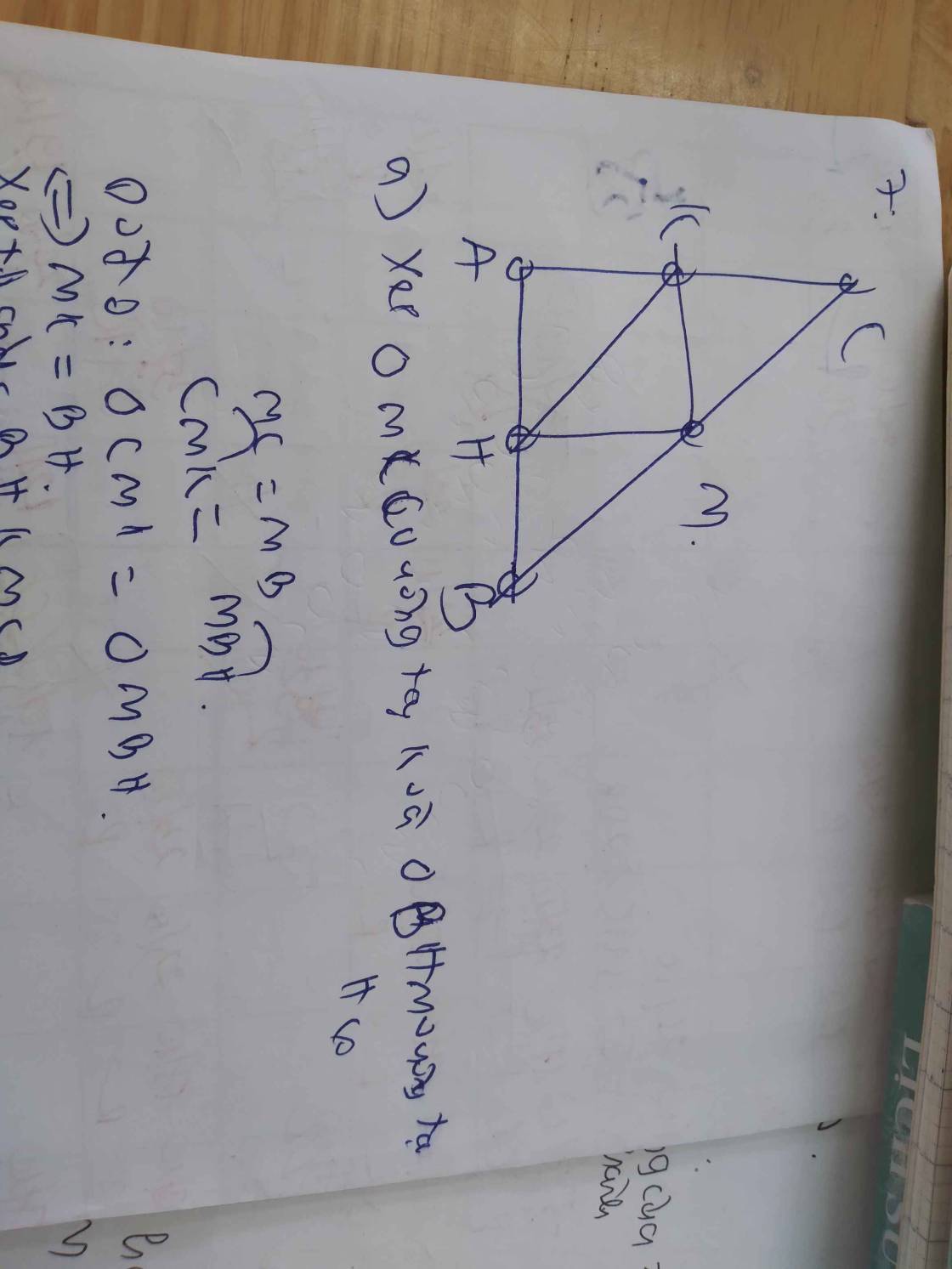
Cho tam giác ABC vuông tại A có đường trung tuyến AM.Kẻ MH⊥AB,MK⊥AC
a) Chứng minh : tứ giác AKMH là hình chữ nhật
b) E là trung điểm MH. Chứng minh tứ giác BHKM là hình bình hành
c) Chứng minh 3 điểm B,E,K thẳng hàng
d) Gọi F là trung điểm của MK . Đường thẳng HK cắt AE tại I và AF tại J.Chứng minh : HI=KJ
Mik cần gấp câu c nha mn