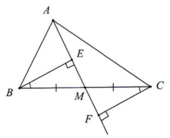
Cho tam giác ABC vuông tại A. Tia Ax đi qua trung điểm M của BC. Kẻ BE và CF cùng vuông góc với Ax ( E thuộc Ax, F thuộc Ax). Chứng minh:
a)Chứng minh tam giác AOM =tam giác BOM
b) chứng minh AM = BM
c) qua H thuộc tia Ot, kẻ đường cuông góc với Ot, nó cắt Ox và Oy theo thứ tự tại C và D
Chứng minh AB song song CD