Cho hai đường tròn (O; R) và (O'; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO'. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; r) theo thứ tự tại C và D (khác A)
a) Chứng minh rằng AC = AD
b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB
c, Kẻ đường kính AE của đường tròn (O) và đường kính AF...
Đọc tiếp
Cho hai đường tròn (O; R) và (O'; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO'. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; r) theo thứ tự tại C và D (khác A)
a) Chứng minh rằng AC = AD
b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB
c, Kẻ đường kính AE của đường tròn (O) và đường kính AF của (O') . Chứng minh rằng bốn điểm E,K,B,F thẳng hàng và OO' song song với È
d, Chứng minh K là trrung điểm của EF
ΔPBO
ΔPBO
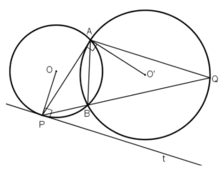
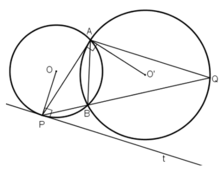
b: Gọi giao của AB và OO' là M
=>M là trung điểm của AB và OO' vuông góc với AB tại M
Xét ΔABK có AM/AB=AI/AK
nên MI//BK
=>BK vuông góc với AB
c:
Xét (O) có
ΔABE nội tiếp
AE là đường kính
DO đó: ΔABE vuông tại B
Xet (O') có
ΔABF nội tiếp
AF là đường kính
Do đó; ΔABF vuông tại B
=>BF vuông góc với AB
góc EBF=góc EBA+góc FBA=90+90=180 độ
=>E,B,F thẳng hàng(1)
góc ABE+góc ABK=90+90=180 độ
nên E,B,K thẳng hàng(2)
Từ (1), (2) suy ra E,B,K,F thẳng hàng