Trên hình 11 có các đường thẳng nào song song với OC?Vì sao?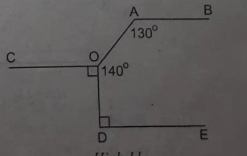
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tương tự 1A
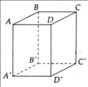
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')

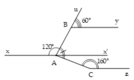
Kẻ tia Ax' là tia đối của tia Ax
Khi đó:
x ' A B ^ = u B y ^ = 60 °
⇒ A x ' // B y
Cũng có:
x ' A C ^ = 80 ° − 60 ° = 20 ° .
⇒ x ' A C ^ + A C z ^ = 180 °
⇒ A x ' // C z .
Do đó các tia A x , B y , C z nằm trên ba đường thẳng song song với nhau

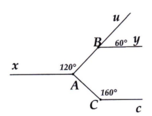
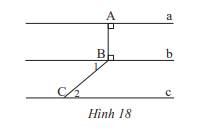
a) Vì a,b cùng vuông góc với đường thẳng AB nên a // b
b) Vì \(\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )\). Mà 2 góc này ở vị trí so le trong nên b // c ( Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì a // b, b //c nên a // c





Có DE // OC góc sole trong bằng nhau (90°=90°)
COA+COD+AOD=360°
=> COD=360°- 90°-140°=130°
Mà BAO=130°=> BAO=COD. 2 góc ở vị trí sole trong lên AB//OC