Cho hàm số y=F(x) thỏa mãn :
f(x)+2f (1 phần x) = X2 +1
tính f(2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TV
1
Những câu hỏi liên quan
CM
18 tháng 11 2017
Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
CM
1 tháng 5 2018
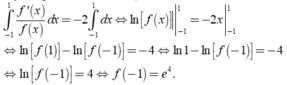
Chọn D.
Đặt u = x + 1 d v = f ' ( x ) d x ⇒ d u = d x v = ∫ f ' ( x ) d x
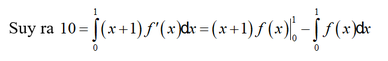
⇔ 10 = 2f(1) – f(0) – I ⇔ 10 = 2 – I ⇔ I = -8.
KN
22 tháng 11 2019
hàm số f(x) xác định với mọi x thỏa mãn \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)nên:
+) x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=\frac{1}{9}\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=\frac{2}{9}\)(1)
+) x = \(\frac{1}{3}\)thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=9\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{-79}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{-79}{27}\)
KN
22 tháng 11 2019
Làm ngược, sửa:))
+) Nếu x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=9\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(1)
+) Nếu x = \(\frac{1}{3}\) thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{161}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{7}\)
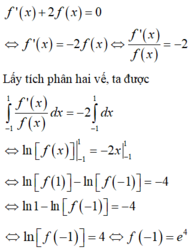
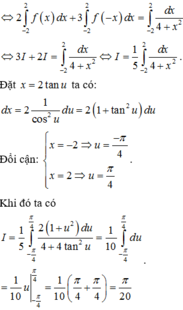
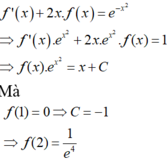
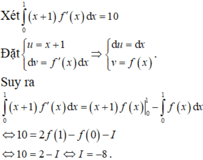
Thay lần lượt \(x=2\) và \(x=\dfrac{1}{2}\) vào ta được:
\(\left\{{}\begin{matrix}f\left(2\right)+2.f\left(\dfrac{1}{2}\right)=2^2+1\\f\left(\dfrac{1}{2}\right)+2.f\left(\dfrac{1}{\dfrac{1}{2}}\right)=\left(\dfrac{1}{2}\right)^2+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}f\left(2\right)+2.f\left(\dfrac{1}{2}\right)=5\\f\left(\dfrac{1}{2}\right)+2f\left(2\right)=\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2f\left(\dfrac{1}{2}\right)+f\left(2\right)=5\\2f\left(\dfrac{1}{2}\right)+4f\left(2\right)=\dfrac{5}{2}\end{matrix}\right.\) \(\Rightarrow3f\left(2\right)=\dfrac{5}{2}-5=\dfrac{-5}{2}\)
\(\Rightarrow f\left(2\right)=\dfrac{-5}{6}\)