Hàm số \(y=x^5-2x^3+1\) có bao nhiêu điểm cực trị?(toán lớp 12)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A.
Đặt u = x 2 - 2 x , ta có y = f u ⇒ y ' = 2 x - 2 f ' u = 2 x - 2 f ' x 2 - 2 x .
Do đó, phương trình y ' = 0 ⇔ [ 2 x - 2 = 0 x 2 - 2 x = - 2 x 2 - 2 x = - 1 x 2 - 2 x = 0 ⇔ [ x - 1 3 = 0 x 2 - 2 x + 2 = 0 x 2 - 2 x = 0 ⇔ [ x = 0 x = 1 x = 2 .
Vậy hàm số đã chốc 3 điểm cực trị là x = 0; x= 1; x = 2.

Đáp án D
f ' ( x ) = 0 ⇔ ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 = 0 ⇔ x = 1 x = - 1 x = - 3 2
Xét dấu:
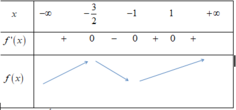
Vậy hàm số có 2 cực trị
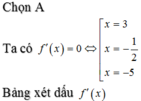

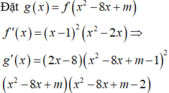
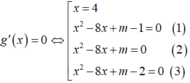





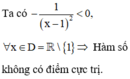
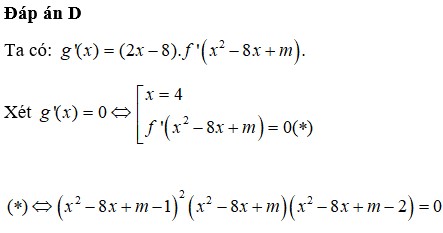
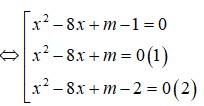

Ta có :
\(y' = 5{x^4} - 6{x^2} = {x^2}\left( {5{x^2} - 6} \right) \Rightarrow y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = \pm \sqrt {\frac{6}{5}} } \end{array}} \right.\)
Ta có : \(y'=5x^4-6x^2=x^2\left(5x^2-6\right)\)
\(\Rightarrow y'=0\Leftrightarrow\hept{\begin{cases}x=0\\x=\pm\sqrt{\frac{6}{5}}\end{cases}}\)
Bảng :
Vậy hàm có 2 điểm cực trị