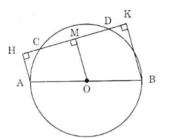
Cho đường tròn O đường kính AB, dây CD ko cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B dến CD. Chứng minh rằng CH= DK
Giúp mình với ngày kia phải thi nên cần câu trả lời gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 12 2019
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)
CM
5 tháng 1 2018
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)
CM
28 tháng 5 2018
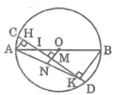
Kẻ OM ⊥ CD cắt AD tại N
Ta có: MC = MD (đường kính dây cung)
Hay MH + CH = MK + KD (1)
Ta có: OM // BK (cùng vuông góc với CD)
Hay: MN // BK
Mà: OA = OB (= R)
Suy ra: NA = NK (tính chất đường trung bình của tam giác)
Lại có: OM // AH (cùng vuông góc với CD)
Hay: MN // AH
Mà: NA = NK (chứng minh trên)
Suy ra: MH = MK (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: CH = DK
KD
25 tháng 4 2017
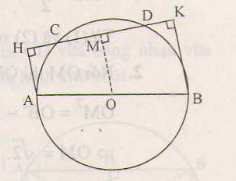
Vẽ ta được CM=DM. (1)
Ta có OM // AH //BK (cùng vuông góc với CD).
Mặt khác , OA=OB nên MH=MK. (2)
Từ (1) và (2) suy ra CH=DK.
Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.
23 tháng 10 2018
VẽOM⊥CDta được CM=DM. (1)
Ta có OM // AH //BK (cùng vuông góc với CD).
Mặt khác , OA=OB nên MH=MK. (2)
Từ (1) và (2) suy ra CH=DK.
Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.
HH
20 tháng 1 2021
Ta có : \(AH\perp CD\left(gt\right)\)
\(BK\perp CD\left(gt\right)\)
=> AH // BK
=> Tứ giác ABKH là hình thang có đáy AH và BK
Theo ( gt ) : OA = OB mà \(OM\perp CD\)( theo cách dựng )
=> OM // AC / BK
=> MK = MH (1)
Mặt khác : \(OM\perp CD\Rightarrow MC=MD\left(2\right)\)
Từ (1) và (2) => MH - MC = MK - MD
=> CH = DK
Vậy CH = DK
28 tháng 4 2021
Lời giải chi tiết
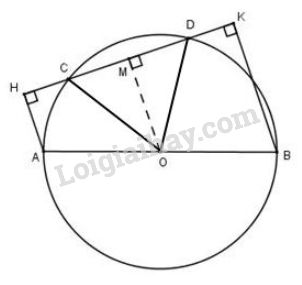
Vẽ OM⊥CDOM⊥CD
Vì OM là một phần đường kính và CD là dây của đường tròn nên ta có M là trung điểm CD hay MC=MDMC=MD (1) (định lý)
Tứ giác AHKBAHKB có AH⊥HK; BK⊥HK⇒HA//BKAH⊥HK; BK⊥HK⇒HA//BK.
Suy ra tứ giác AHKBAHKB là hình thang.
Xét hình thang AHKBAHKB, ta có:
OM//AH//BKOM//AH//BK (cùng vuông góc với CDCD)
mà AO=BO=AB2AO=BO=AB2
⇒MO⇒MO là đường trung bình của hình thang AHKBAHKB.
⇒MH=MK⇒MH=MK (2)
Từ (1) và (2) ⇒MH−MC=MK−MD⇔CH=DK⇒MH−MC=MK−MD⇔CH=DK (đpcm)
Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm CC và DD cho nhau.
Hình: Tự vẽ
Vì CD không cắt đường kính AB=> CD<AB<=>H;K nằm ngoài đường tròn
Từ O ta kẻ OF vuông góc với CD tại F
=>F là trung điểm của CD (t/c của đường kính tương ứng với dây cung)
=>CF=DF(cmt)
Vì AH vuông góc với CD
và BD vuông góc với CD =>AH//BD(từ vuông góc đến song song)
=> Hình thang AHDB(dhnb)
Mà OF vuông góc CD tại F
=> OF//AH//BD
Vì O là tâm đường kính AB
=> O là trung điểm của AB )=>F là trung điểm của HK
và OK//AH
=>FH=FK(cmt)
Mà CF+HC=HF
FD+DK=FK
có HF=FK;CF=FD
=>HC=DK(điều phải chứng minh)