cho xyz bằng 1 tính: A=\(\dfrac{x}{xy+x+1}+\dfrac{y}{yz+y+1}+\dfrac{z}{zx+z+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????

\(=\dfrac{xy\left(z-1\right)-y\left(z-1\right)-x\left(z-1\right)+\left(z-1\right)}{xy\left(z+1\right)+y\left(z+1\right)-x\left(z+1\right)-\left(z+1\right)}\\ =\dfrac{\left(z-1\right)\left(xy-y-x+1\right)}{\left(z+1\right)\left(xy+y-x-1\right)}=\dfrac{\left(z-1\right)\left(x-1\right)\left(y-1\right)}{\left(z+1\right)\left(x+1\right)\left(y-1\right)}=\dfrac{\left(z-1\right)\left(x-1\right)}{\left(z+1\right)\left(x+1\right)}\\ =\dfrac{\left(5003-1\right)\left(5001-1\right)}{\left(5003+1\right)\left(5001+1\right)}=\dfrac{5002\cdot5000}{5004\cdot5002}=\dfrac{5000}{5004}=\dfrac{1250}{1251}\)


\(B=\dfrac{x+2xy+1}{x+xy+xz+1}+\dfrac{y+2yz+1}{y+yz+ỹ+1}+\dfrac{z+2zx+1}{z+zx+zy+1}\)
\(B=\dfrac{yz\left(x+2xy+1\right)}{yz\left(x+xy+xz+1\right)}+\dfrac{xz\left(y+2yz+1\right)}{xz\left(y+yz+ỹ+1\right)}+\dfrac{xy\left(z+2zx+1\right)}{xy\left(z+zx+zy+1\right)}\)
\(B=\dfrac{\left(1+y\right)+y\left(1+z\right)}{\left(1+y\right)\left(1+z\right)}+\dfrac{\left(1+z\right)+z\left(1+x\right)}{\left(1+z\right)\left(1+x\right)}+\dfrac{\left(1+x\right)+x\left(1+y\right)}{\left(1+x\right)\left(1+y\right)}\)
\(B=\dfrac{y}{1+y}+\dfrac{1}{1+z}+\dfrac{1}{1+x}+\dfrac{z}{1+z}+\dfrac{1}{1+y}+\dfrac{x}{1+x}\)
\(B=\left(\dfrac{y}{1+y}+\dfrac{1}{1+y}\right)+\left(\dfrac{1}{1+z}+\dfrac{z}{1+z}\right)+\left(\dfrac{x}{1+x}+\dfrac{1}{1+x}\right)\)
\(B=1+1+1\)
\(B=3\)

Lời giải:
Từ \(xy+yz+xz=xyz\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
Đặt \((a,b,c)=\left(\frac{1}{x}; \frac{1}{y}; \frac{1}{z}\right)\Rightarrow a+b+c=1\)
BĐT cần chứng minh trở thành:
\(P=\frac{c^3}{(a+1)(b+1)}+\frac{a^3}{(b+1)(c+1)}+\frac{b^3}{(c+1)(a+1)}\geq \frac{1}{16}(*)\)
Thật vậy, áp dụng BĐT Cauchy ta có:
\(\frac{c^3}{(a+1)(b+1)}+\frac{a+1}{64}+\frac{b+1}{64}\geq 3\sqrt[3]{\frac{c^3}{64^2}}=\frac{3c}{16}\)
\(\frac{a^3}{(b+1)(c+1)}+\frac{b+1}{64}+\frac{c+1}{64}\geq 3\sqrt[3]{\frac{a^3}{64^2}}=\frac{3a}{16}\)
\(\frac{b^3}{(c+1)(a+1)}+\frac{c+1}{64}+\frac{a+1}{64}\geq 3\sqrt[3]{\frac{b^3}{64^2}}=\frac{3b}{16}\)
Cộng theo vế các BĐT trên và rút gọn :
\(\Rightarrow P+\frac{a+b+c+3}{32}\geq \frac{3(a+b+c)}{16}\)
\(\Leftrightarrow P+\frac{4}{32}\geq \frac{3}{16}\Leftrightarrow P\geq \frac{1}{16}\)
Vậy \((*)\) được chứng minh. Bài toán hoàn tất.
Dấu bằng xảy ra khi \(a=b=c=\frac{1}{3}\Leftrightarrow x=y=z=3\)

\(T=\dfrac{\left(xy\right)^2}{zx+zy}+\dfrac{\left(yz\right)^2}{xy+xz}+\dfrac{\left(zx\right)^2}{yx+yz}\ge\dfrac{xy+yz+zx}{2}\ge\dfrac{3}{2}\sqrt[3]{\left(xyz\right)^2}=\dfrac{3}{2}\)
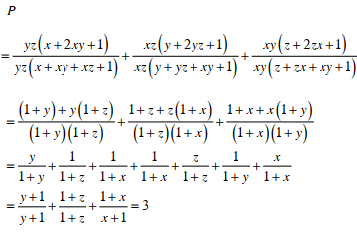
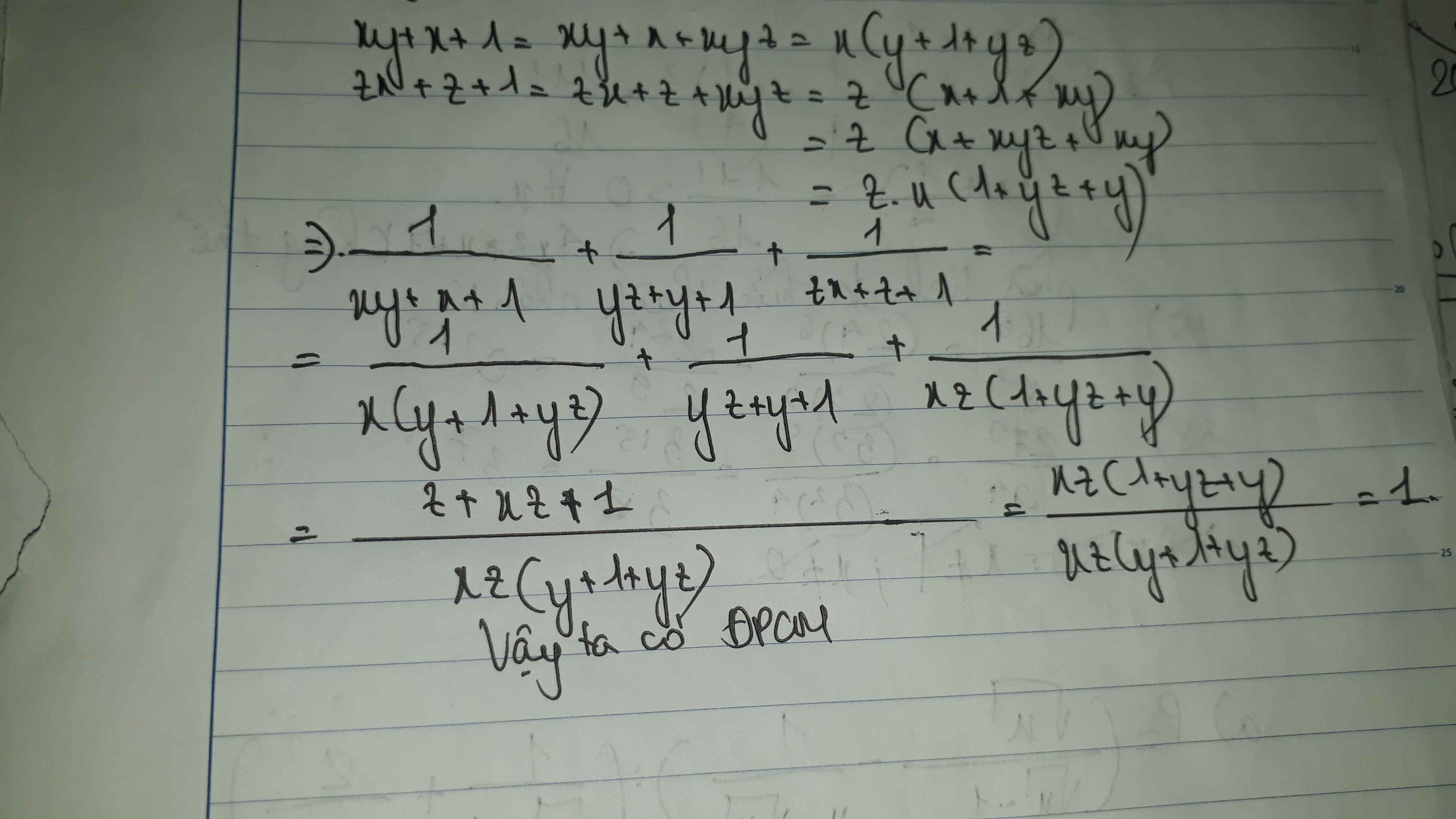
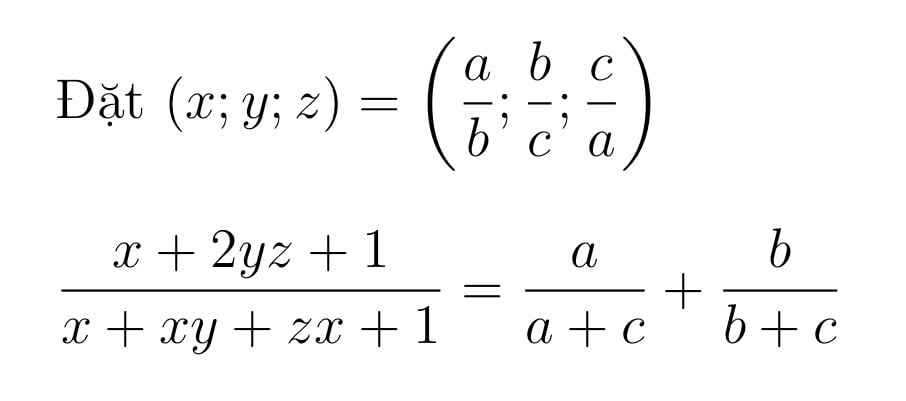
Câu hỏi của jgfhjudfhuvfghdf - Toán lớp 8 | Học trực tuyến