CMR: A= [ n3( n2 -7)2 -36n ] ⋮ 7 ∀ n∈ Z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=n\left[n^2\left(n^2-7\right)^2-36\right]=n\left[\left(n^3-7n\right)^2-36\right]\)
\(=n\left(n^3-7n-6\right)\left(n^3-7n+6\right)\)
\(=n\left(n-3\right)\left(n+1\right)\left(n+2\right)\left(n-2\right)\left(n-1\right)\left(n+3\right)\)
\(\Rightarrow A\) là tích 7 số nguyên liên tiếp nên A luôn chia hết cho 7

Ta có
A =n[n2(n2 -7)2 -36]= n[(n3 -7n2)-36]
= n(n3 -7n2 -6)( n3 -7n2 +6)
Mà n3 -7n2 -6 = (n+1) (n+2) (n-3)
n3 -7n2 +6 = (n-1)(n-2)(n+3)
Do đó:
A= (n-3)(n-2)(n-1)(n+1)(n+2)(n+3)
Đây là tích của 7 số nguyên liên tiếp.Trong 7 số nguyên liên tiếp
+Tồn tại một bội của 5 ⇒ A chia hết cho 5
+Tồn tại một bội của 7 ⇒ A chia hết cho 7
+Tồn tại hai bội của 3 ⇒ A chia hết cho 9
+Tồn tại ba bội số của 2,trong đó có một bội số của 4 ⇒ A chia hết cho 16
A chia hết cho các số 5,7,9,16 đôi một nguyên tố cùng nhau nên A chia hết cho
5.7.9.16 =5040.
+ Qua ví dụ 1 rút ra cách làm như sau:
Gọi A(n) là một biểu thức phụ thuộc vào n (n ∈ N hoặc n ∈ Z).
n^3-n^2+2n+7=(n^3+n)-(n^2+1)+n+8=n(n^2+1)-(n^2+1)+n+8. Để n(n^2+1)-(n^2+1)+n+8 chia hết cho n^2+1=>8+n chia hết cho n^2+1
Vậy n=2k hoặc 2k+1
Xét TH:n=2k
=>8+n=8+2k(1)
*n^2+1=(2k)^2+1=4k^2+1(2)
Từ (1) và (2) ta có:8+2k chia hết cho 2 mà 4k^2+1 không chia hết cho 2 nên n ko bằng 2k
Xét TH:n=2k+1=>8+n=8+2k+1(3)
*n^2+1=(2k+1)^2+1
n^2+1=(4k^2+1)+(2k+1)(4)
Từ 3 và 4 : muốn 8+n chia hết n^2 +1 thì 8 chia hết cho 4k^2+1
=>4k^2+1 thuộc{-1;+1;-2;+2;-4;+4;-8;8}
các bạn làm từng TH thì sẽ ra k=0 và n=1 và các bạn thế vào đề bài lai để kiểm tra kết quả



Vì đây là 7 số nguyên liên tiếp
nên A chia hết cho 7!
=>A chia hết cho 5040

Có A = [ n3 (n2 -7 )2 -36n ]
= n [ n2 (n2 -7)2 - 36] = n[ n(n2 -7) -6][n(n2-7) +6]
= n( n3 -7n -6)(n3 -7n +6) = n(n3 -n -6n -6)(n3 -n -6n +6)
= n[ n( n2-1 ) - 6(n+1)][ n( n2 -1)-6(n-1)] = n[ n(n-1)(n+1) -6(n+1)][ n(n-1)(n+1)-6(n-1)]
= n [ (n+1)(n2 -n-6)][ (n-1)(n2 +n -6)] = n[ n(n-3)(n+1) +2(n-3)][n(n+3)(n-1) - 2(n+3)]
= n(n+1)(n-3)(n+2)(n-1)(n+3)(n-2)
mà n; (n+1); (n-3); (n+2); (n-1); (n+3); (n-2) là 7 STN liên tiếp => A⋮ 7 ∀ n∈ Z


Vì đây là 7 số nguyên liên tiếp
nên A chia hết cho 7

\(n^3\cdot\left(n^2-7\right)^2-36n\)
\(=\left(n-3\right)\cdot\left(n-2\right)\cdot\left(n-1\right)\cdot n\cdot\left(n+1\right)\cdot\left(n+2\right)\cdot\left(n+3\right)\)
Đây là 7 số tự nhiên liên tiếp
Trong 7 số tự nhiên liên tiếp sẽ có một số chia hết cho 7
\(\Rightarrow Biểu\) thức trên chia hết cho 7 với mọi \(n\in Z\)
Hay \(n^3\cdot\left(n^2-7\right)^2-36n⋮7\left(\forall x\in Z\right)\)

Ta có 5040 = 24. 32.5.7
A= n3(n2- 7)2 – 36n = n.[ n2(n2-7)2 – 36 ] = n. [n.(n2-7 ) -6].[n.(n2-7 ) +6]
= n.(n3-7n – 6).(n3-7n +6)
Ta lại có n3-7n – 6 = n3 + n2 –n2 –n – 6n -6 = n2.(n+1)- n (n+1) -6(n+1)
=(n+1)(n2-n-6)= (n+1 )(n+2) (n-3)
Tương tự : n3-7n+6 = (n-1) (n-2)(n+3)
Do đó A= (n-3)(n-2) (n-1) n (n+1) (n+2) (n+3)
Ta thấy : A là tích của 7 số nguyên liên tiếp mà trong 7 số nguyên liên tiếp:
- Tồn tại một bội số của 5 (nên A chia hết 5 )
- Tồn tại một bội của 7 (nên A chai hết 7 )
- Tồn tại hai bội của 3 (nên A chia hết 9 )
- Tồn tại 3 bội của 2 trong đó có bội của 4 (nên A chia hết 16)
Vậy A chia hết cho 5, 7,9,16 đôi một nguyên tố cùng nhau A 5.7.9.16= 5040

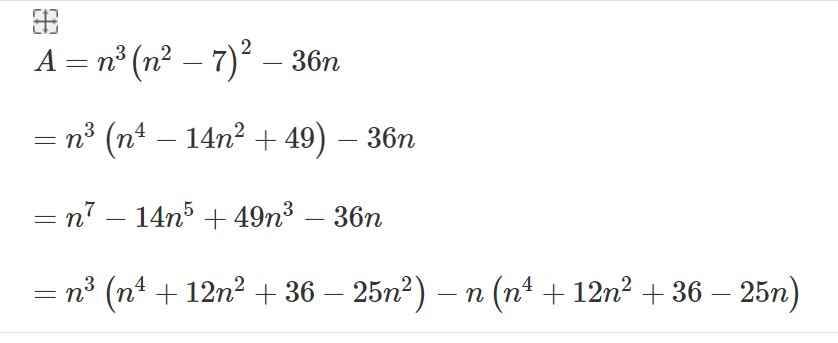
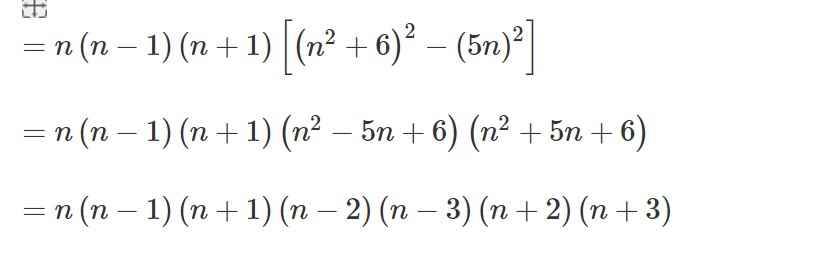
Vì đây là 7 số liên tiếp nên A chia hết cho 7!
=>A chia hết cho 105

Vì đây là 7 số nguyên liên tiếp
nên A chia hết cho 7