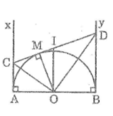
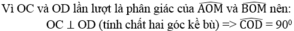cho nửa đường tròn tâm O đường kính AB = 2R. Kẻ các tiếp tuyến Ax, By cùng phía với nửa đường tròn O đg kính AB . Vẽ bán kính OE bất kì . Tiếp tuyến vơi nửa đg tròn tại E cắt Ax,By theo thứ tự ở C,D
a, cmr CD= AC + BD
b, tính số đo góc COD và cm: R2 = AC . BD
C, Tính diện tích tứ giác CDBA theo bán kính R của đg tròn O , bt AC = R/2
kẻ cho mik hình nha mn ><
giúp mik vs , mik đag cần gấp